The day of the last hypothesis would also be the day of the last observation.…An hypothesis which becomes dispossessed by new facts dies an honorable death; and if it has called up for examination those truths by which it is annihilated, it deserves a moment of gratitude.

Jacob Henle (1809–1885)

In foveate animals, the purpose of eye movements is to bring visual stimuli into the peripheral field of vision (peripheral retina) to the central point of best visual acuity (fovea) and to maintain foveal fixation of a moving object. The acquisition (gaze shifting) and securing (gaze holding) of stationary object images on the fovea and the stabilization of images on the fovea during head movement (gaze holding) or target movement (gaze shifting) constitute the basic functions of human eye movements. Although many specific types of eye-movement abnormalities require sophisticated recording and analysis techniques, there are clinical tests that, when properly applied, can provide valuable information about diagnosis, pathophysiologic mechanism, or response to therapy.¹

The ocular motor system can be conceptualized as two independent major subsystems, version and vergence, acting synergistically (Fig. 1).² The version subsystem mediates all conjugate eye movements, whereas the vergence subsystem mediates all disjugate eye movements. Fixation and vestibuloocular inputs influence the version subsystem. At the most peripheral level, regardless of input, there are only three major categories of eye movement output: fast eye movements (FEM or saccades) and slow eye movements (SEM) from the version subsystem and vergence eye movements (VEM) from their own subsystem. All three outputs share a common neural pathway from the ocular motor neurons to the muscles (Fig. 2). In addition, the version subsystems share a common neural network that integrates (mathematically) velocity information into position signals. The fast mode of the version subsystem mediates all conjugate saccades (FEM), and the slow mode mediates all SEM. The latter includes, but is not limited to, the pursuit function. Without knowledge of the conditions that were used to elicit a particular response, one could not differentiate (1) the eye movement record of a voluntary saccade from a nystagmus fast phase or (2) the record made by pursuit of a slowly moving target from that of slow rotation of the subject while fixating a stationary target. The many terms used to describe eye movements generally specify the eliciting input, the functional subsystem, or the circumstance of occurrence, but the eye movements themselves consist of one or more of the three main outputs (FEM, SEM, VEM) of the ocular motor system (Table 1).

TABLE 1. Eye-Movement Classifications

There is ample physiologic, anatomic, and clinical justification for regarding the subsystems as autonomous. However, the neurons within the oculomotor, trochlear, and abducens nuclei are not specific for types of eye movement. Rather, different firing patterns of homogeneous neuronal pools determine the type of eye movement.³

The simplified schema described previously, which uses the three unique ocular motor outputs as a basis for conceptualization of the ocular motor system, is used in this introductory chapter for purely pedagogic reasons. Our approach to the ocular motor system has undergone continuous refinement since its inception in 1974² and has served as the introduction to ocular motility for many medical students, ophthalmology and neurology residents and fellows, biomedical engineering undergraduate and graduate students, and postdoctoral fellows. We have attempted to present an overview of the functional mechanisms thought to comprise the ocular motor system with minimum inclusion of putative anatomical sites or physiological mechanisms. This chapter should provide clinicians with an basic understanding of this complex motor system and students of ocular motility with a solid foundation on which to expand their knowledge base. For the latter, we recommend these textbooks containing the anatomy, physiology, and functional mechanisms of ocular motility in greater detail.^4–6

If one used inputs rather than outputs as a basis for conceptualizing the ocular motor system, the latter could be divided into additional subsystems separated by phylogenetic origins and physiologic modes of action. From an evolutionary point of view, the vestibular subsystem probably developed first, closely followed by the optokinetic and saccadic subsystems; the latter are required to generate reflex fast (quick) phases associated with passive head movement and “afoveate” saccades for active head movement. With the development of a fovea came subsystems for fixation, pursuit, and voluntary saccades and finally the vergence subsystem for binocular single vision and stereopsis. Because the neurophysiologic substrates and varied purposes of these subsystems result in specific properties and limitations, their origins and individual modes of action are key to a complete understanding of the ocular motor system and are especially important if one wishes to study them in situ or with the use of computer models. Observations indicate that a distinct subsystem may mediate the SEM of fixation in synergy with the saccadic and pursuit subsystems. Studies of the latter⁷ and of human congenital nystagmus^8–10 have provided evidence in support of a separate fixation subsystem. Some of the quantitative characteristics of a fixation or “stabilization” subsystem have begun to be elucidated.^11–13 The different inputs, outputs, and components of these subsystems are discussed in the sections of this chapter dealing with the major output subsystem to which they belong (i.e., FEM, SEM, or VEM).

Fast eye movements are rapid version (conjugate) eye movements that are under both voluntary and reflex control. Examples of voluntary saccades are willed refixations and those in response to command (e.g., “Look to the right…Look up.”). The sudden appearance of a peripheral visual object or an eccentric sound may evoke a reflex saccade in the direction of the stimulus. In the natural state, a head movement in the same direction usually accompanies these saccades. However, in clinical examinations and in most physiologic experiments, the head is stabilized.

The visual stimulus for FEM is target (object) displacement in space. After an instantaneous change in target position, the ocular motor system will respond with a FEM after a latency (delay) of 200 to 250 milliseconds. Both the peak velocity and the duration of FEM are dependent on the size (amplitude) of eye movement, which varies from 30°/second to 800°/second and 20 to 140 milliseconds, respectively, for movements from 0.5° to 40° in amplitude. FEM are conjugate and ballistic. The control system responsible for their generation is discrete. At discrete instants in time, control decisions are made based on the continuous inflow of visual information from the retina. In normal persons, these decisions are essentially irrevocable; once the eyes are in motion, their trajectory cannot be altered. The control signal is retinal error (disparity of image position from the fovea), which is automatically reduced to zero by the nature of negative feedback.

After the appropriate latency, the FEM response to target displacement (Fig. 3) consists of a period of acceleration to a peak velocity and then deceleration of the eyes as they approach the new target position. The muscular activity in the agonist–antagonist pair of each globe is characterized by a burst of maximal facilitation in the agonist and total inhibition in the antagonist during the movement (Fig. 4). Electromyographic (EMG) recordings reveal that FEM deceleration is usually not consequent to active braking by the antagonist muscle. Rather, the two muscles merely assume the relative tensions necessary to hold the new target position. This is sufficient to accomplish the rapid deceleration because of the braking effect (damping) of the “ocular motor plant” (i.e., globe, muscles, check ligaments, and fatty supporting tissue of the orbit). EMG recordings have identified active dynamic braking in the antagonist muscles for some saccades. The active braking seems to be associated more often with small saccades than with large saccades. Occasionally a saccade is of such magnitude that it overshoots the target, and a saccade in the opposite direction follows it without latency; this is called a dynamic overshoot. Dynamic overshoots are common in both voluntary and involuntary (e.g., the fast phases of nystagmus) saccades. There is also evidence that with an unrestricted head, intersaccadic latencies may be reduced.¹⁴

The overdamped plant (mechanical resistance of orbital structures) requires that the neural signal necessary to achieve the rapid FEM acceleration must be a high-frequency burst of spikes, followed by the tonic spike frequency required to stop and then hold the eyes at the new position. This combination of phasic and tonic firing patterns is designated the “pulse-step” of neural innervation (Fig. 5). The eye movement in Figure 5A results from a step change in neural firing frequency and, reflecting the overdamped plant dynamics, is considerably slower than a normal FEM. A normal FEM trajectory occurs only when a pulse precedes the step (see Fig. 5B). A neural “pulse generator” and “integrator” combine to form the required pulse-step of innervation (Fig. 6). The pulse generator consists of burst cells, whose activity is normally inhibited by pause cells (see Fig. 6). When the pause cells cease firing, the burst is turned on, and the duration of its high-frequency pulse of innervation is determined by a feedback circuit that contains a second, resettable neural integrator.¹⁵ This resettable neural integrator, within the pulse generator, feeds back a signal that simultaneously turns off the burst cells and reactivates the pause cells. The resettable neural integrator of the pulse generator is not the same as the common neural integrator used to generate the tonic innervation levels sent to the ocular motor nuclei. Because there are pathologic conditions (e.g., gaze-evoked nystagmus) that affect the ability of the eyes to maintain gaze but do not alter the trajectory of saccades, two separate neural integrators seem to be required: a resettable integrator within the pulse generator that functions to set pulse width, and a second, common integrator that is responsible for generating the constant level of tonic innervation required to maintain gaze.^15,16 This hypothesis of normal saccade generation was supported by ocular-motility studies of common human clinical conditions. Almost a decade passed before neurophysiologic studies in animals provided additional supportive evidence.¹⁷ The pulse generator for horizontal eye movements is located within the pontine paramedian reticular formation (PPRF) at the level of the abducens nuclei, specifically, in the nucleus pontis caudalis centralis (see Chapter 10, Fig. 4).¹⁸ Vertical burst neurons are located in the rostral interstitial nucleus of the medial longitudinal fasciculus (MLF). The superior colliculus is intimately involved in the generation of saccades, especially short-latency “express” saccades.¹⁹ Projections to the superior colliculus come from the frontal, parietal, and occipital cortex; projections from the superior colliculus go to areas in the brainstem reticular formation containing the saccadic burst and omnipause neurons. The superior colliculus appears to contain signals equivalent to motor error and may include the resettable integrator.^20–25 The existence of the resettable neural integrator has also been questioned.²⁶ Thus, despite the concerted efforts of several groups, the location of the resettable neural integrator or its equivalent remains a topic of speculation and competing hypotheses 30 years after it was first hypothesized. The horizontal common integrator may be located in the nucleus prepositus hypoglossi, the medial vestibular nucleus, and possibly other (cerebellum) locations. The vertical integrator is probably in the interstitial nucleus of Cajal.²⁷ The location of the summing junction for the pulse and step is uncertain but must be prenuclear with respect to the third cranial nerve because MLF axons carry neural information that is already summated (pulse plus step).²⁸ Both burst neurons (pulse) and tonic neurons (step) project to an area of the nucleus of the abducens nerve, where intranuclear interneurons project to the nucleus of the oculomotor nerve via the MLF. Thus, the summing junction is probably in the area of the nucleus of the abducens nerve.

Because saccades are not always accurate and their trajectories are not always normal, a scheme has been devised to describe both their metrics and trajectories. The pulse-step of innervation necessary to make a saccade is used to define what is meant by orthometric, hypometric, or hypermetric eye movements. The final gaze position that the eye assumes (after the effects of both the pulse and step) is used to measure saccadic accuracy. The step determines metrics, and the relationship between the pulse and step determines the trajectory (i.e., the way in which the eye arrives at its final position). Saccades may be either orthometric, hypometric, or hypermetric and may have numerous trajectory variations. The latter have been identified as normal, slow, overshoot, undershoot, dynamic overshoot, discrete decelerations, and multiple closely spaced saccades. A complete description of a particular saccade must include both metrics and trajectory; a refixation may include several saccades of varying metrics and trajectories. A thorough discussion of saccadic metrics along with a recursive shorthand notation for metrics and trajectories may be found in Schmidt et al.²⁹ All the possible departures from the norm of the saccadic system were derived from and illustrated in Schmidt's article on myasthenia gravis.

Other factors may influence the speed of saccades; both attention and state of convergence can play a role. Saccades made under conditions of increased demand for accuracy are slower than normal.³⁰ This has been found to be associated with increased co-contraction of the extraocular muscles, presumably increasing the stiffness of the plant, both statically and dynamically.³¹ The discovery of fibromuscular “pulleys,” through which the extraocular muscles pass, provides a mechanism by which this can be accomplished.³² These compliant pulleys are under active control and can change the effective moment arm of the muscles, thereby altering the dynamics of the resulting eye movement.

The closed-loop nature of the FEM mode of the version subsystem can be depicted in a simplified block diagram (Fig. 7) containing only primary signal paths and lacking the paths containing the control signals that appear to be necessary to simulate known ocular motor responses of both normals and those with dysfunction due to either congenital or acquired conditions. The conjugate retinal error signal, representing a discrepancy between target and eye position, is sensed in the cerebral cortex. Signals derived from this information are used in the brain stem to generate the neural command to the ocular motor neurons necessary for the FEM, which moves the eye to its new position, thereby reducing the retinal error to zero (foveal fixation).

The FEM subsystem can be modeled as a discontinuous or, more specifically, a sampled-data control system in which visual information is used during sample intervals (intermittent sampling). Between samples, new visual information, although perceived, cannot be used to modify any eye movement decisions. The study of patients with pathologically slow saccades has revealed that under these conditions it is possible to modify a saccade in flight based on new visual information.³³ A detailed presentation of the control-system analysis of the various types of eye movements is beyond the scope of this chapter.

Rapid eye movements (REM) of paradoxical sleep and the fast phases of evoked (vestibular, optokinetic) or pathologic nystagmus are also examples of saccadic eye movements. These saccades and those of refixation share the same physiologic characteristics.

During a saccade, the visual threshold is elevated about 0.5 log units (saccadic suppression). This phenomenon is controversial; some investigators postulate an active central inhibitory process,³⁴ whereas others³⁵ favor a retinal-image “smear” mechanism. In either case, the relatively small visual threshold elevation cannot account entirely for the subjective sense of environmental stability during saccades. A mechanism, designated “corollary discharge” or “efference copy,” in which the visual system is “altered” centrally (by way of fronto-occipital connections) for forthcoming retinal image movement probably serves to cancel conscious perception of environmental motion during a saccade.³⁶

The saccadic system, as well as other ocular motor systems, is plastic (i.e., its gain is under adaptive control based on feedback signals that monitor its performance). Although saccades are programmed in the brain stem, their size is controlled by means of cerebellar circuits, and it is these circuits that change saccadic gain in response to neurologic deficits. By alternately patching one eye in a patient with a third nerve palsy and studying the gain of the saccadic system as it varied with time, Abel et al.³⁷ documented the plastic gain changes in the saccadic system and measured the time constants of this adaptation. The time constants were found to be on the order of 1 to 1.5 days; both the duration of the innervational pulse and the magnitude of the step were adjusted independently.

One of the ways in which the cerebellum is thought to make parametric adjustments in the saccadic system is by varying the amount of position information fed back to the input of the common neural integrator (Fig. 8). Because this neural integrator is an imperfect one (i.e., it cannot hold its output without a decay in the signal, referred to as a “leak”), the gain (K_c) of the position feedback is adjusted to overcome its inherent leakiness. By using eye-position feedback, the cerebellum evaluates the performance of the common neural integrator, and adjustments in K_c are made. Problems either in the neural integrator itself or in this parametric adjustment circuitry can cause various types of nystagmus. If K_c is too small, the inherent leakiness of the neural integrator will cause the eyes to gradually drift back toward primary position from any eccentric gaze position. If K_c is too high, the eyes will accelerate centrifugally away from the desired gaze position with an ever-increasing velocity until reset by a centripetal saccade.

During evaluation of the ocular motility of a patient, the eye movements seen are a result of both the initial insult and the plastic adaptation that has resulted; if the insult is to the structures involved in system plasticity, either hypometric or hypermetric activity is possible.

The major stimulus for pursuit in foveate animals is a fixated target that moves; this evokes a pursuit SEM after a latency of 125 milliseconds. The maximum sustained pursuit velocities are about 90°/second,³⁸ although higher values can be obtained for large-amplitude, full-field, or self-moved target motions.³⁹ The SEM of the vestibuloocular reflex (VOR) and of optokinetic nystagmus (OKN) or congenital nystagmus (CN) can be considerably faster. SEM are conjugate, smooth, and under a control system capable of continuous modification of motor output in response to visual input (in contrast to discrete FEM control). The input signal is retinal error (“slip”) velocity, which is reduced to zero when eye velocity matches target velocity. The work of Yasui and Young⁴⁰ suggests that retinal slip velocity is used along with corollary discharge to recreate a target velocity signal, and it is this “perceived target velocity” that drives the SEM system. This would provide an explanation for many of the “pursuit” responses to nonmoving targets (e.g., afterimages). True pursuit is an SEM in response to a moving target. There are many other ways to elicit SEM (see Table 1), and further study is required to uncover other mechanisms. Under normal conditions, a moving target is usually required for a pursuit SEM; attempts to move the eyes smoothly without actual target motion result in a series of small saccades.⁴¹

When a foveated target suddenly moves at a constant velocity, the pursuit response begins after a 125-millisecond latency (Fig. 9). The initial movement is the same velocity as the target, but because of the latency, the eyes are behind the target and require a catch-up saccade for refoveation while continuing the tracking with a pursuit SEM. The catch-up saccade follows the initiation of the pursuit movement because of the longer latency of the FEM subsystem. Plant dynamics do not permit a simple linear increase (ramp) in neural firing frequency to rapidly accelerate the eyes to the velocity of the moving target (see Fig. 5C); a “step-ramp” of innervation is needed (see Fig. 5D). Thus, an instantaneous jump in firing frequency (the step) is followed by a linear increase in frequency (the ramp). It is commonly accepted that the same neural integrator used to generate the tonic firing level necessary for FEM is used for the step-ramp of SEM. Like FEM, the SEM subsystem is a closed loop with negative feedback (Fig. 10). The conjugate retinal error signal (slip velocity) is sensed at the visual cortex, and this information is used in the brain stem to generate the required pursuit SEM to reduce the retinal error velocity to zero. Target position, target velocity, and retinal slip velocity have all been related to the generation of smooth pursuit movements, but none of these alone adequately accounts for all the observed characteristics of pursuit SEM. Efferent eye position, velocity information, or both are probably used in addition to the aforementioned stimuli. The role of target acceleration in smooth pursuit is in dispute.^42,43

Because the FEM mode responds to target-position errors and the SEM mode to target-velocity errors (real or perceived), what would be the response to a sudden imposition of both types of error? Experiments using step-ramp (Rashbass) stimuli (i.e., the target simultaneously steps to a new position and assumes a constant velocity in the direction opposite its step of displacement) have shown that the pursuit SEM mode is independent of, but synergistic with, the FEM mode of the dual-mode version subsystem. Thus, the pursuit system will cause tracking in the direction of target motion at 125 milliseconds, despite the target displacement in the opposite direction; that displacement will be corrected by a saccade at 200 milliseconds as tracking continues.

Although retinal image velocity is the main stimulus for pursuit, there is ample evidence that position error also plays a role.^44,45 By responding to both position and velocity, the pursuit system can maintain the target image on the fovea with little or no retinal slip velocity.^46–48 Finally, pursuit is influenced by a predictive mechanism that permits target tracking with a minimal phase lag and, in some cases, with a phase lead.^49–51

Maintaining the image of a target of interest within the foveal area is the function of the fixation subsystem. Although it has been suggested that fixation is not active during smooth pursuit,¹¹ our studies of congenital nystagmus foveation suggest that fixation works synergistically to maintain target foveation during pursuit. Although it may not be true that fixation is pursuit at zero velocity, as Yarbus⁴¹ suggested, we hypothesize that pursuit includes fixation at, or near, zero position (i.e., when the pursuit and saccadic subsystems have positioned the target within the foveal area). Current data suggest that maintenance of target foveation is accomplished by velocity control (similar to smooth pursuit).¹² However, we believe that some position control is also present to maintain the target in the center of the foveal area, where acuity is maximal. This would mimic the presence of position control during smooth pursuit.⁴⁴

Head movement is the stimulus for the VOR. The latency between the onset of sudden head movement and the resultant SEM can be as little as 15 milliseconds. The peak velocities of vestibuloocular SEM are also variable and may be as fast as 300 to 400°/second. The movements are conjugate and smooth, and the control system is continuous, but unlike the closed-loop saccadic and pursuit functions, the vestibuloocular system is an open loop (Figs. 11 and 12). The control signal is head acceleration transduced by the semicircular canals to a neural signal proportional to head velocity. The canals thus perform the mathematical step of integration necessary to convert acceleration to velocity. The velocity information enters the vestibular nuclei, which project to the ocular motor neurons (Fig. 11). The final step of mathematical integration that converts velocity data to the position signal may take place in the vestibular nuclei, nucleus prepositus hypoglossi, or both. In Figure 12 the open-loop vestibuloocular function is diagrammed such as would occur in darkness with no visual inputs. Final eye position is therefore equal to relative eye position plus head position.

The gain of the VOR (eye velocity/head velocity) is about 1 and does not vary much in the range of normal head movements (less than 7 Hz). Similarly, the phase shift is small, in the region of 0.01 to 7 Hz. In the dark, when doing mental arithmetic, a subject's VOR gain is about 0.65 at 0.3 Hz, but in the light, or when asked to look at an imaginary spot on the wall in total darkness, the gain rises to 1 and 0.95, respectively. Thus, to raise the natural gain of the VOR from 0.65, the subject must be attending to the environment. Unfortunately, below 0.01 Hz the gain and phase of the VOR change rapidly with frequency. Thus, for very slow movements, the VOR is not useful; low-frequency movements are discussed in the section on the optokinetic reflex (OKR). Because the time constant of the cupula is about 4 seconds, the low-frequency range of the VOR should not extend below 0.03 Hz. However, the fact that it does extend down to 0.01 Hz is due to a lengthening of the effective VOR time constant from the 4 seconds of the cupula to about 16 seconds. This is done in the vestibular nuclei, the cells of which exhibit the 16-second time constant rather than the cupula time constant. With head-on-body movement, input from neck receptors summates with input from the vestibular end-organ to produce compensatory eye movement.⁵² For simplicity, we have not included this nuchal-ocular function in our block diagrams.

The OKR is responsible for filling in where the VOR fails (i.e., at the low end of the frequency spectrum of head and body movements). Proper excitation of the optokinetic system requires movement of the entire visual surround. This is most easily observed in afoveate animals (such as the rabbit) that do not track small moving targets. Whereas in real life it is self-motion that stimulates the OKR, in the laboratory the OKR is more easily studied by placing the subject within a moving surround. When this surround begins to move, the eyes will begin to follow in the same direction after a latency of a little more than 100 milliseconds, and eye velocity will slowly build to a value equal to that of the surround. In humans, because of a well-developed pursuit system, this slow buildup of eye velocity is not seen, and the eyes quickly assume a velocity equal to that of the surround. It is extremely difficult to study the isolated OKR in humans because of our well-developed pursuit system and the fact that the OKR reaches maximum velocity at a different velocity than the pursuit system. If one studies the eye movements that result in darkness after an optokinetic stimulus is removed (optokinetic after-nystagmus–OKAN), the effects of the pursuit system are removed and the basic OKR can be evaluated. Because of their complementary time constants (and, therefore, frequency responses), the OKR and VOR act synergistically during self-rotation to induce eye movements that are equal and opposite to motion of the surround. This joint activity is evidenced anatomically by the fact that the optokinetic signals (which are velocity commands) are mediated through the vestibular nuclei.

Because of their synergistic interaction as well as their virtual inseparability in normal head and body motions in a lighted environment, the VOR and OKR are usually combined as the visual-vestibuloocular response. With the addition of vision (Fig. 13), a feedback loop is closed around the open-loop VOR, and what results is the visual-vestibuloocular response. The ability of the ocular motor system to relate eye position to target position in situations of head movement is thereby markedly enhanced for quick (high-frequency) movements of the head and for sustained rotation. Thus, the ocular motor system is able to accurately move the eyes opposite the moving environment.

Early studies of the saccadic system in normals,⁵³ as well as later studies of abnormalities in the saccadic system,⁵⁴ suggested that the FEM subsystem contained an internal monitor of efferent eye-position commands that is used to generate subsequent saccades. By combining retinal error position with the internal copy of eye position, a reconstructed target-position signal is used by the pulse generator to generate a saccade. The signals fed back by this internal monitor come from the output of the common neural integrator and enter the saccadic system at a point before the sampling that characterizes the saccadic system. This is not the feedback signal used in the actual generation of the pulse by the pulse generator (see earlier discussion). Similarly, studies of the pursuit system⁴⁰ have suggested that an internal monitor is used to feed back eye-velocity commands. By this mechanism, the pursuit system would reconstruct target velocity and generate a velocity command to the eyes that was based on that signal rather than on retinal slip velocity. These studies supported the hypothesis contained in the first behavioral model of the ocular motor system that exhibited internal oscillations, such as congenital nystagmus; that is, efference copy was necessary for the proper operation of the ocular motor system.^55–57 Figure 14 shows a simplified block diagram of the internal monitor and its connections in both the FEM and SEM subsystems. The reconstructed target signals, both position (θ_T') and velocity (dθ_T'/dt), are used to generate both position and velocity commands to the eyes.

Large FEM (greater than 15°) are often inaccurate, necessitating corrective movements to bring the eyes on target. After a latency of about 125 milliseconds, saccadic corrective movements follow inaccurate (dysmetric) conjugate refixation saccades. Corrective saccades are conjugate and occur even in darkness, thereby precluding any significant role of visual feedback information.⁵³ The exact mechanism responsible for these saccadic corrective movements is uncertain, but the internal monitor of eye position is probably involved. In addition, proprioceptive feedback remains a plausible explanation, despite the ongoing controversy about the existence and importance of proprioception from the extraocular muscles.

Disjugate dysmetric refixation saccades usually involve one accurate eye, with the other either undershooting or overshooting. The dysmetric eye is brought to the target by a slow (usually less than 20°/second) movement, designated a “glissade.”⁵³ The glissade results from a mismatch between the pulse and the step of the original saccade. Rather than a purposive corrective movement, a glissade is a passive drift dictated by the viscoelastic properties of the plant (orbit).

The stimulus for VEM is target displacement or motion along the visual Z-axis (toward or away from the observer). Vergence latency is about 160 milliseconds, maximum velocities are in the range of 20°/second, and the movements are disjugate and smooth. VEM control is continuous, and the inputs are retinal blur (open loop) or diplopia (closed loop). The VEM subsystem is asymmetric (i.e., convergence movements are faster than divergence movements) and is uniquely capable of generating a uniocular eye movement. The time course is similar to that depicted in Figure 5A for a step change in target position and in Figure 5C for a constant target velocity. Thus, VEM outputs simply reflect innervational signals on the overdamped plant dynamics. The VEM subsystem is a closed loop when diplopia is the error signal (Fig. 15). The step (of innervation) command from the midbrain generator to the ocular motor neurons results in appropriate VEM to reduce diplopia to zero.

When eye movements are studied in the laboratory or evoked in clinical examinations, individual types are isolated by fixation of the head and/or provision of a simple appropriate stimulus. However, most naturally occurring eye movements are a combination of various version movements admixed with VEM, reflecting the synergistic operation of all the subsystems (Fig. 16). Although it was previously presumed that compound eye movements to targets with both conjugate and disjugate errors (e.g., targets with both horizontal and depth differences) were merely the sum (at the ocular motor nuclei) of separately programmed conjugate and disjugate eye movements, we now know that the saccadic and vergence synergism occurs at a lower level, producing disjugate saccades that accomplish the different required uniocular movements.^58,59 Thus, a saccades from a near to a distant target (requiring divergence) would result in an adduction-abduction asymmetry greater than the slight asymmetry of purely horizontal saccades (abduction is of greater initial velocity than adduction, causing transient divergence followed by convergence). When convergence is required, as when looking from a distant to a near target, the asymmetry is decreased. Because accomplishing these differences in uniocular eye movement is more efficiently done during the saccade, such asymmetrical saccades are more prevalent under natural conditions than under laboratory conditions, where conjugate and disjugate movements are usually studied separately.⁶⁰ Finally, there are interactions between vergence and vertical saccades with transient horizontal divergence associated with upward and convergence with downward, movements.⁶¹ Disjugate saccadic eye movements support the hypothesis of a uniocular control architecture (see “Unilateral and Bilateral-Yoked Control”).

Underactivity or overactivity in any of the ocular motor subsystems may result in dynamic eye-movement disturbances (Fig. 17). These constitute abnormal ocular oscillations, of which nystagmus is the most common. Increasing the delay in the visual feedback pathway induces low-frequency oscillations in normals and superimposes such oscillations on the higher frequency oscillations of acquired pendular nystagmus.^62,63 The latter observation suggests that acquired pendular nystagmus is due to instability of an internal feedback loop in the ocular motor system (see Chapter 11).

Humans and other primates possess an intricate synergism linking accommodation, convergence, and pupillary constriction, an interrelationship variably termed “near response,” “near reflex,” “near-point triad,” or “near synkinesis” (also see Chapter 15). The near triad can be elicited by electrical stimulation of the cerebral cortex at the junction of the occipital and temporal lobes (Brodmann's area 19). Although abolition of any one of the functions does not interfere with the others, there is a definite causal relationship among the three phenomena. Pupillary constriction is directly dependent on both the convergence impulse and the accommodative impulse. As Figure 18 illustrates, the near triad is composed of three closed-loop subsystems, the signals of which are linked to their respective motor controllers. Thus, the accommodative signal also affects the pupil-lary and vergence motor controllers, and the vergence signal affects the accommodative and pupillary motor controllers. The net result is activity causing a response in each of the systems, whether the stimulus is image blur, light, disparity (diplopia), or any combination of the three. Because pupil diameter directly affects the depth of field of focal planes, a dotted feedback path has been included from the output of the pupillary system to the input of the accommodative system. Although the pupillary response to light is closed loop, its function in the near response is essentially open loop because of the small influences of blur and disparity on pupil diameter.⁶⁴

Sensitive recording techniques during fixation of a stationary target disclose three types of eye movements less than 1° in amplitude: microsaccades, microdrift, and microtremor.⁴¹ Microsaccades (flicks) are conjugate, although often of unequal amplitude in the two eyes. They range from 1 to 25 minutes (average of 6 minutes) of arc and demonstrate a velocity-amplitude relationship analogous to that of refixation saccades. The frequency of microsaccades is about 1 to 3 Hz. Microdrifts are disjugate and slow, with speeds varying from 1 to 30 minutes of arc/second. Microtremor constitutes a disjugate, high-frequency vibration of the eyes, ranging from 50 to 100 Hz, with amplitudes varying from 5 to 15 seconds of arc.

The significance of these micromovements is uncertain. It was originally believed that both microsaccades and drifts played a corrective role in fixation,⁶⁵ but later studies have indicated that microsaccades probably do not occur naturally and are unique to eye movement recording conditions.⁶⁶

Optical methods that stabilize retinal images completely, thereby eliminating the effect of micromovements, result in complete image fade-out after several seconds.⁴¹ This implies that the small eye movements (especially tremor), by continuously sweeping images across several receptors, prevent cone saturation. The characteristics of the various types of eye movements are summarized in Table 2.

TABLE 2. Eye-Movement Characteristics

Most models of ocular motor control, including those in this chapter, are reduced to their simplest form. That is, they are unilateral in architecture with precise yoking presumed. Although such models are limited to simple, stereotyped responses, they are useful for many types of studies and for pedagogic purposes.

Unilateral, yoked control (UYC) models contain both positive and negative signals, despite the bilateral nature of brain stem organization and the positive-only nature of neuronal signals. UYC models have one eye and are essentially monocular representations of perfectly yoked eyes. As such, they cannot duplicate many of the properties of the physiologic system that are a function of internal interconnections. One basic tenet of control system theory is that behavior is a function of interconnections (feedback loops) and not the gains of individual elements. Studies of the bilateral nature of ocular motor control required expansion (duplication) of the UYC models into bilateral yoked control (BYC). In these, perfect yoking is still assumed, but neuronal signals are positive, as are their physiologic counterparts. The “push-pull” interconnections across the midline can be modeled with BYC architecture.⁶⁷

Studies of normal and, especially, abnormal eye movements of humans and of dogs and humans with absent optic chiasms suggest independent control of each eye. This directly implies independent control of each eye muscle,⁶⁸ which is due to the bilateral architecture of the brain stem. A bilateral independent control (BIC) model evolves from this data. A BIC model is necessary to model the ocular motor control of a chameleon, for instance. To include binocularity, yoking must be added to BIC, producing a bilateral, yoked, independent control (BYIC) model. Figure 19 shows such a model and includes the saccadic and pursuit subsystems; the addition of the four fixation, four VOR, four OKN, and vergence subsystems would greatly increase the complexity of a BYIC model, as can be seen by comparing Figure 19 with Figure 11 (minus the vestibular input).

In the past 50 years, there have been many “models” proposed for either isolated functional blocks (within an ocular motor subsystem), individual subsystems, or more rarely, the complete ocular motor version (or vergence) system for a given plane. Models fall into either the “bottom-up” (for isolated blocks) or “top-down” (subsystem and system models) category. The top-down approach is taken in this chapter but the block-diagram figures cannot be considered true models unless each block can be defined mathematically or simulated on a computer. The bottom-up approach has been favored by those whose research involves single-cell neurophysiology, whereas the top-down approach is more common to those whose approach is based on control systems and whose models are required to mimic robustly a broad range of human behavioral ocular motor responses to controlled target inputs (i.e., the characteristics of the responses to specific target inputs must simulate those of normal individuals). Besides this differentiation, some models are based solely on data from “normals” (either humans or animals), whereas the foundations of others also include “abnormal” data (i.e., data from patients and animals with ocular motor abnormalities). Restricting a model's foundations to normal data often fails to uncover important mechanisms in the ocular motor system and, more importantly, leads to models that are oversimplified and cannot simulate even the most rudimentary responses to simple abnormalities.

Our modeling has been guided by the philosophy that by studying ocular motor system abnormalities we would uncover hidden normal mechanisms and abilities not possible from studies of normals alone. We use the following criteria to guide our modeling: (1) all models of dysfunction must duplicate known normal ocular motor behavior; (2) all putative mechanisms for dysfunction must simulate the behavioral responses of patients with the disorder being modeled in addition to the abnormal waveforms (e.g., nystagmus or saccadic dysfunctions); (3) merely simulating waveforms in isolation may be an interesting homework problem for a control system engineer but, even if the model contains “realistic,” “physiological” mechanisms, it is not good enough and, until such putative mechanisms can be shown to actually work within a top-down, behavioral model, they must remain highly suspect; and (4) putative mechanisms must be tested within a complete, behavioral model containing all relevant subsystems, even those not directly involved in the simulated behavior, to ensure there are neither unexpected interactions nor behaviors. The brain is a highly complex organ and the ocular motor system is a multiloop, multifunction control system with specialized subsystems, each also complex.

A top-down model is invaluable in the conceptualization of how the overall system works and how it fails in the face of specific types of dysfunction. Given the long time intervals required for the bottom-up approach to modeling to arrive at universally agreed upon anatomic sites or models for small portions of subsystems, the expectation that it is capable of producing a total behavioral model of ocular motility in the near future is problematic. Taken to its limit, the restriction that all models be anatomically and neurophysiologically “accurate” at the neuronal or cellular level leads to a model of the size and complexity approaching that of the brain itself, something requiring computer power not yet available and cortical power not likely to evolve. Therefore, we regard the development and use of top-down behavioral models as imperative to continued progress in studying ocular motor function and dysfunction.

We have attempted to adhere to these principles in the computer models of dysfunction we have made. Beginning with a behavioral model of the ocular motor system containing the internal oscillation of congenital nystagmus,^55–57 later models of gaze-evoked nystagmus,¹⁵ Alexander's law,⁶⁷ and myasthenia gravis⁶⁹ expanded on the concept of an internal monitor coordinating the operation of the various subsystems responsible for responses to saccadic, pursuit, and combinations of the two stimuli. A behavioral model of the version portion of the ocular motor system evolved that is capable of simulating many normal and abnormal behaviors.^6,70–76 Figure 20 is the block diagram of the present model, containing both primary signal paths (thick lines) and the essential signal paths (thin lines) responsible for logical decisions and the control of the various functional blocks. The model contains many of the functional blocks discussed in this chapter and includes one large block that is necessary if a model is to fulfill the criteria stated earlier. That block, the internal monitor, grew in size and complexity from its precursors to perform additional functions required for the accurate simulation of behavioral ocular motor responses in the presence of a wide variety of acquired and congenital dysfunctions. Put simply, the internal monitor is the “brains” of the model. It calculates reconstructed eye and target position and velocity, provides the Alexander's law variation to tonic imbalances, coordinates subsystem responses, and makes the necessary logical decisions that enable the model's output, whether during simulation of normal or abnormal behavior, to duplicate what has been recorded from the respective humans when subjected to specific target input while viewing with a fixed head.

Figure 21 demonstrates how the current version simulates the behavioral responses of normal individuals. The responses to small target steps (top left panel) are accurate and occur with the normal saccadic latency. As the target steps become larger (top right panel), the simulations consist of a hypometric saccade followed by a short-latency corrective saccade, mimicking normal responses. The responses to very short (30 ms) pulse changes in target position (middle left panel) are steps to the second target position, ignoring the short initial position; this too, mimics normal responses. For longer (100 ms) pulse inputs (middle right panel), the response consists of two saccades separated by the normal intersaccadic interval. For each type of pulse input, the initial saccades exhibit normal latencies. The model's responses to target ramps (bottom left panel) exhibit both the normal smooth pursuit accuracy and latency. Responses to target step-ramps exhibit the normal pursuit and saccadic latencies and accuracies, demonstrating the synergistic action of these subsystems. The model is also capable of simulating both these behavioral responses and the waveforms of individuals with gaze-evoked nystagmus, myasthenia gravis (and Lambert-Eaton syndrome), the fusion maldevelopment nystagmus syndrome (latent/manifest latent nystagmus) with Alexander's law variation, the infantile nystagmus syndrome (congenital nystagmus), square-wave jerks/oscillations, square-wave pulses, saccadic dysmetria, and staircase saccadic intrusions⁷⁷ (see Chapter 11). We are currently incorporating a visual-vestibular subsystem to allow simulations during head and environmental motion.

Most published models have been limited to small portions of specific subsystems or to suggest putative mechanisms for a specific waveforms of nystagmus. No attempts were made to assess the effects on the behavior of the ocular motor system if these mechanisms were inserted into a complete behavioral model. Without such evaluations, hypothetical mechanisms generating specific waveforms remain highly speculative. One use of a robust, behavioral model of the ocular motor system is to test proposed mechanisms of dysfunction by integrating them into the model and determining their effects on all responses. We designed this model to be modular, which will facilitate testing of specific functional blocks with a replacement that is claimed to be an improvement. Another benefit of a behavioral model is that it allows testing of mechanisms hypothesized to cause the deviations from normal behavior exhibited by patients with specific disorders.

Eye-movement recording is required for quantitative information and as a permanent record in both basic research and clinical situations.

In one early technique of recording eye movements, a series of images was placed on the retina by regularly flashing lights. This necessitated subjective verbal reports, yielded no permanent record, and was replaced by mechanical recording devices.

Historically, mechanical transducers represented an improvement over the afterimage method in that a permanent record was obtained. They involved the attachment of instruments to the eye that interfered with normal eye movements. More sophisticated techniques are now used.

Motion picture recording of eye movements is an excellent, simple technique for gross clinical comparisons and teaching purposes. However, there are a number of compelling limitations in the use of photography for quantitative recordings. It is extremely time consuming and requires careful frame-by-frame analysis, large quantities of expensive film, and rigid head mounting.

Corneal reflection is an offshoot of direct photography and involves photographing a light reflected on the cornea. The light beam is focused on a photographic film to provide permanent records. The use of photographic film prevents real-time monitoring of the data, but this limitation can be overcome by television scanning. The head must be rigidly stabilized for quantitative recording, because considerable error is introduced with slight head movement. The system is linear and accurate within a narrow range of amplitude and is suitable for quantitative recording of micromovements of the eye. Although not suitable for clinical purposes, it is an excellent technique for recording the scanning patterns of subjects viewing scenes or pictures.

The contact lens method, which usually involves reflecting a beam of light from a mirror mounted on a corneal contact lens, is extremely sensitive and can measure eye movements of less than 10 seconds of arc, making it useful for the recording of micromovements.

Because of different metabolic rates, the cornea is about 1 mV positive with respect to the retina, a situation that creates an electrostatic field that rotates with eye movement. Skin electrodes placed around the eye can therefore record eye position. Although both eyes can be averaged with the use of bitemporal electrodes, this method does not result in correct eye-position information about either eye and therefore can be very misleading. We recommend that each eye be measured separately with periorbital electrodes. Recording only one eye is preferable to bitemporal electrodes if only one channel is available; at least the movements of that eye will be recorded without the contamination that results from bitemporal electrode placement. Electro-oculography (EOG) is useful and convenient for recording eye movements from about 1° to 40°, but frequent calibration is essential because of nonlinearities and baseline drift.

Alternating-current-coupled EOG is a simple method of recording nystagmus and is used in electronystagmography. However, neither eye position nor slow pursuit can be recorded with the use of alternating-current amplification. For quantitative studies, direct-current oculography is essential. This introduces the problem of baseline drift, which can be overcome partially with strict attention to proper electrode and skin preparation and the use of modern, low-drift, direct-current amplifiers. We recommend alternating-current-coupled EOG only for clinicians who want a recording of spontaneous and caloric-induced nystagmus and are not concerned with quantitative analysis. Satisfactory recordings of vertical eye movements are difficult to perform with EOG because of muscle artifact and eyelid movement.

Photoelectric oculography encompasses a variety of techniques, each involving the projection of light over the cornea and a photosensitive device that responds to the light reflected from the eye. The voltage output from the photo sensors is a function of the angle of gaze. Infrared techniques yield a linear output to ∼20° and are the most commonly used. As in EOG, both eyes can be recorded simultaneously in the horizontal direction. Vertical eye movements can be measured accurately only if eyelid interference is eliminated; this usually restricts the range to ±10°. Compared with EOG, the system is virtually noise free, and its fast dynamic response is advantageous for the recording of saccades. It is useful for measuring eye movements during reading and is a preferred technique in research involving eye movements within 20° of primary position. Infrared photoelectric oculography is, in most respects, preferable to EOG for quantitative recording. Although it has a limited range when recording vertical eye movements, unlike EOG, the measurements are accurate. Because movement of the sensors relative to the eyes can produce artifacts in the eye signal, some systems measure the corneal reflection relative to either the pupil or fourth Purkinje image from the posterior surface of the lens. These systems have had limited success in eye movement monitoring.

The scleral search coil is a wire coil embedded in a contact lens. The subject is placed in an alternating magnetic field, and eye position is recorded from the voltage induced in the coil. This scleral search coil is an accurate technique for both large and small movements.⁷⁸ Contact lens techniques now allow binocular tracings, because occlusion of the recorded eye is no longer required. Although the search coil is very sensitive (5 minutes of arc), has a large range (±90°), and can be used to record both horizontal and vertical eye movements simultaneously at bandwidths up to 500 Hz, it is an invasive technique and therefore of limited clinical utility except in the hands of highly trained personnel. Also, there is some evidence that the coils and their output wires may alter the dynamics of eye movements.⁷⁹ Despite these limitations, it is one of the most accurate and versatile methods available.

With the advent of small, lightweight CCD video cameras with higher scan-rate frequencies, digitization of video signals, and integrated software, eye movements can now be accurately measured and digitally stored by means of a video front end. Horizontal, vertical, and (in some systems) torsional eye movements can be simultaneously recorded by this noninvasive method. Linear ranges of ±40° horizontally and ±30° vertically are possible, with sampling rates up to 500 Hz and noise of less than 0.1°. In comparison to the magnetic search coil, accurate and reliable horizontal and vertical position signals are provided, although the eye velocities were noisier in early models.⁸⁰ Another advantage of the video signal is that the information necessary for pupillary diameter measurements is already present and can be extracted by the appropriate software. The scanning laser ophthalmoscope (SLO) is a special device that makes use of video. The SLO provides a video record of the retina, on which the visual stimulus is superimposed. With appropriate video digitization and software, the SLO can also be used for quantitative analysis.

The methods described previously measure eye position. Electromyography, in which concentric needle electrodes are inserted into the extraocular muscles, records muscle action potentials. The technique is difficult and provides little useful information to the pragmatic clinician. However, it is a research tool that has provided data about eye-movement neurophysiology and explanations of clinical phenomena.

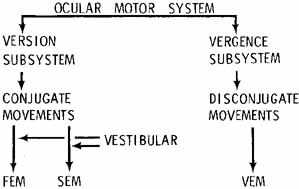
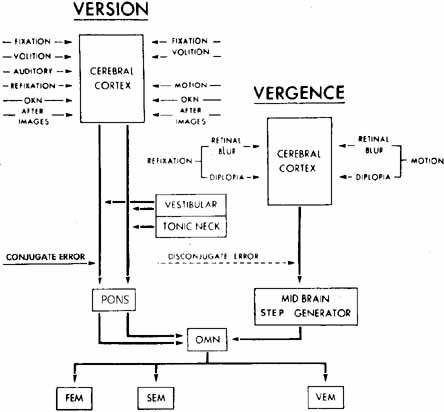
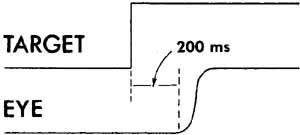
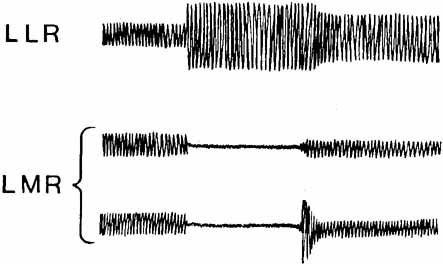
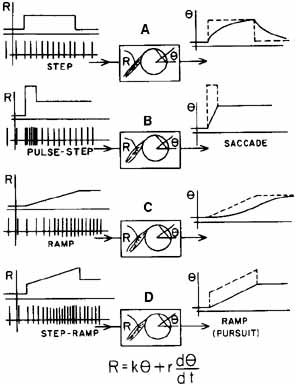
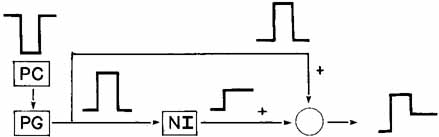
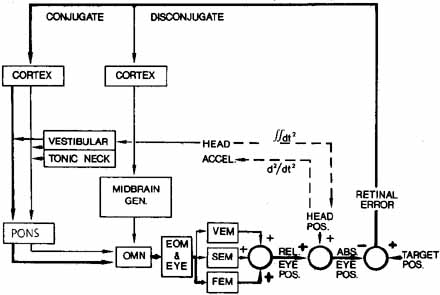
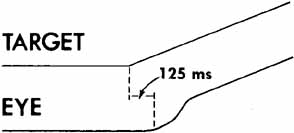
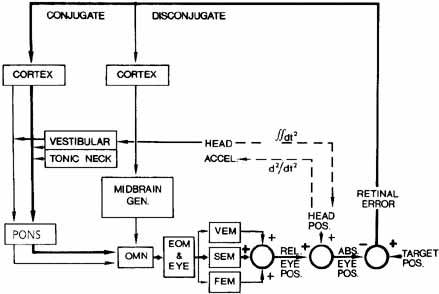
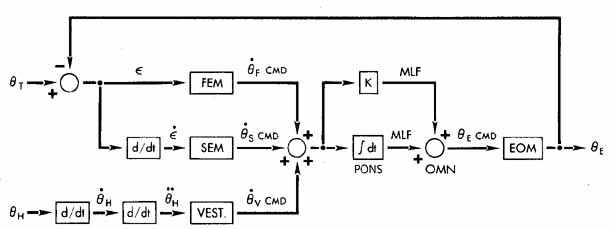
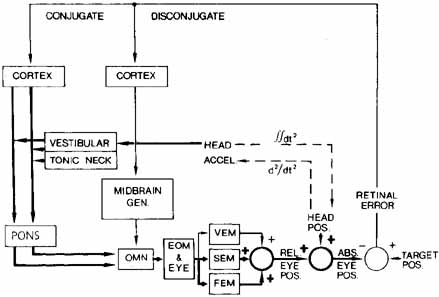
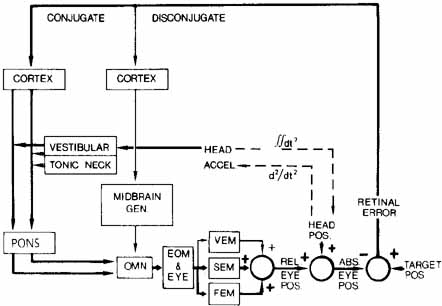
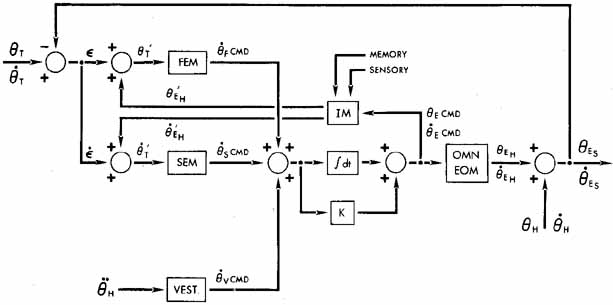
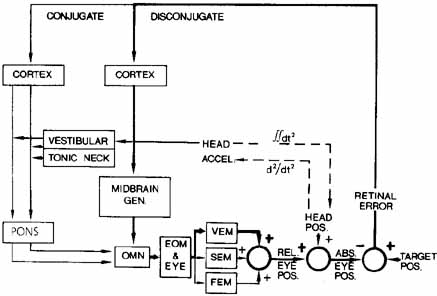
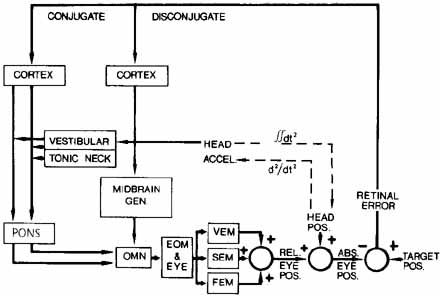
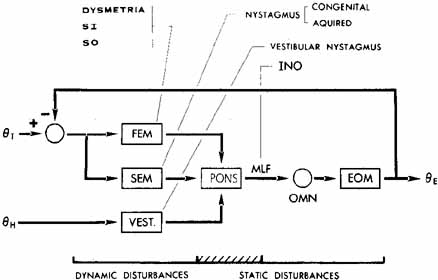
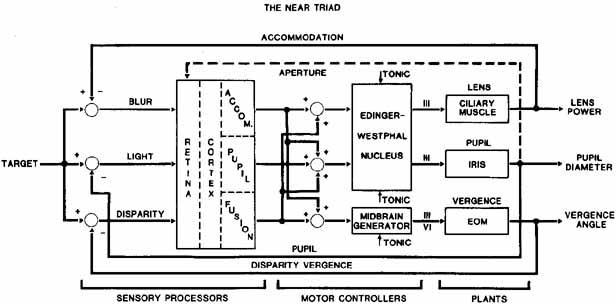
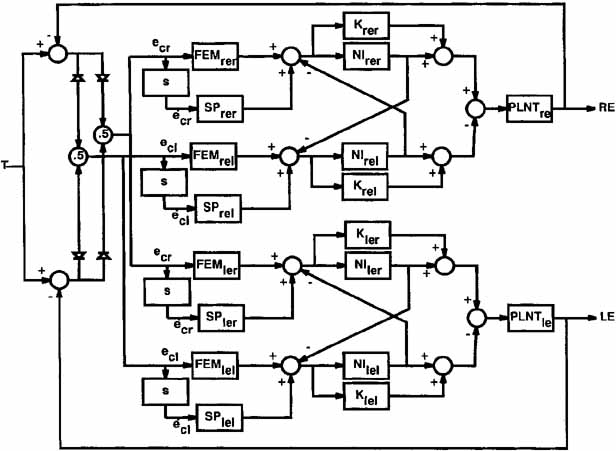
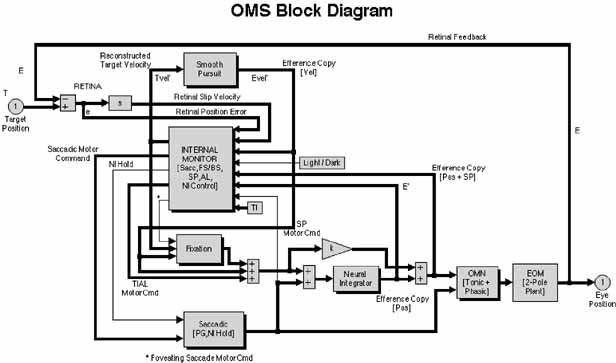
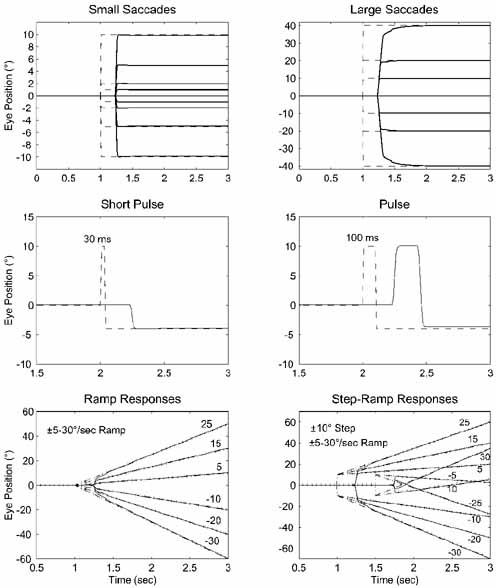
1. Shaunak S, O'Sullivan E, Kennard C: Eye movements. J Neurol Neurosurg Psychiat 59:115, 1995

2. Dell'Osso LF, Daroff RB: Functional organization of the ocular motor system. Aerospace Med 45:873, 1974

3. Keller EL, Robinson DA: Abducens unit behavior in the monkey during vergence movements. Vision Res 12:369, 1972

4. Carpenter RHS: Movements of the eyes. 2nd ed. London: Pion, 1988:1

5. Leigh RJ, Zee DS: The neurology of eye movements (Contemporary Neurology Series). 4th ed. New York: Oxford University Press, 2001:1

6. Dell'Osso LF: Nystagmus basics. Normal models that simulate dysfunction. In Hung GK, Ciuffreda KJ (eds): Models of the visual system. New York: Kluwer Academic / Plenum Publishers, 2002:711

7. Robinson DA, Gordon JL, Gordon SE: A model of smooth pursuit eye movements. Biol Cyber 55:43, 1986

8. Dell'Osso LF: Fixation characteristics in hereditary congenital nystagmus. Am J Optom Arch Am Acad Optom 50:85, 1973

9. Dell'Osso LF, Van der Steen J, Steinman RM, et al: Foveation dynamics in congenital nystagmus I: Fixation. Doc Ophthalmol 79:1, 1992

10. Dell'Osso LF, Van der Steen J, Steinman RM, et al: Foveation dynamics in congenital nystagmus II: Smooth pursuit. Doc Ophthalmol 79:25, 1992

11. Luebke AE, Robinson DA: Transition dynamics between pursuit and fixation suggest different systems. Vision Res 28:941, 1988

12. Epelboim J, Kowler E: Slow control with eccentric targets: evidence against a position-corrective model. Vision Res 33:361, 1993

13. Tusa RJ, Zee DS, Hain TC, et al: Voluntary control of congenital nystagmus. Clin Vis Sci 7:195, 1992

14. Skavenski AA, Steinman RM: Free headed monkeys make saccades at very high frequencies in a novel laboratory environment. Invest Ophthalmol Vis Sci 36:S354, 1995

15. Abel LA, Dell'Osso LF, Daroff RB: Analog model for gaze-evoked nystagmus. IEEE Trans Biomed Engng BME 25:71, 1978

16. Dell'Osso LF, Daroff RB: Clinical disorders of ocular movement. In Zuber BL (ed): Models of oculomotor behavior and control. West Palm Beach: CRC Press Inc, 1981:233

17. Scudder CA: A new local feedback model of the saccadic burst generator. J Neurophysiol 59:1455, 1988

18. Keller EL: Participation of medial pontine reticular formation in eye movement generation in monkey. J Neurophysiol 37:316, 1974

19. Fischer B, Weber H: Express saccades and visual attention. Behav Brain Sci 16:553, 1993

20. Waitzman DM, Ma TP, Optican LM, et al: Superior colliculus neurons provide the saccadic motor error signal. Exp Brain Res 72:649, 1988

21. Van Gisbergen JAM, Van Opstal AJ: Models. In Wurtz RH, Goldberg ME (eds): The neurobiology of saccadic eye movements. Reviews of Oculomotor Research, Vol. 3. Amsterdam: Elsevier, 1989:69

22. Munoz DP, Wurtz RH: Saccade-related activity in monkey superior colliculus. I. Characteristics of burst and buildup cells. J Neurophysiol 73:2313, 1995

23. Munoz DP, Wurtz RH: Saccade-related activity in monkey superior colliculus. II. Spread of activity during saccades. J Neurophysiol 73:2334, 1995

24. Optican L: Control of saccade trajectory by the superior colliculus. In üttner U, et al (eds): Contemporary ocular motor and vestibular research: A tribute to David A. Robinson. Stüttgart: Thieme, 1994:98

25. Optican LM: A field theory of saccade generation: Temporal-to-spatial transform in the superior colliculus. Vision Res 35:3313, 1995

26. Kaneko CRS: Effect of ibotenic acid lesions of the omnipause neurons on saccadic eye movements in rhesus macaques. J Neurophysil 75:2229, 1996

27. Fukushima K, Kaneko CRS, Fuchs AF: The neuronal substrate of integration in the oculomotor system. Prog Neurobiol 39:609, 1992

28. Pola J, Robinson DA: An explanation of eye movements seen in internuclear ophthalmoplegia. Arch Neurol 33:447, 1976

29. Schmidt D, Dell'Osso LF, Abel LA, et al: Myasthenia gravis: Dynamic changes in saccadic waveform, gain and velocity. Exp Neurol 68:365, 1980

30. Hendriks AW, Enright JT: Eye movements become slower with increasing demand for accuracy. Invest Ophthalmol Vis Sci 36:S355, 1995

31. Enright JT, Hendriks AW: Cognitive influence on the relationship between peak velocity and amplitude of saccades. Invest Ophthalmol Vis Sci 36:S597, 1995

32. Demer JL, Miller JM, Poukens V, et al: Evidence for fibromuscular pulleys of the recti extraocular muscles. Invest Ophthalmol Vis Sci 36:1125, 1995

33. Zee DS, Optican LM, Cook JD, et al: Slow saccades in spinocerebellar degeneration. Arch Neurol 33:243, 1976

34. Chase R, Kalil RE: Suppression of visual evoked responses to flashes and pattern shift during voluntary saccades. Vision Res 12:215, 1972

35. Mitrani L, Mateef ST, Yakimoff N: Is saccadic suppression really saccadic? Vision Res 11:1157, 1971

36. Koerner F, Schiller PH: The optokinetic response under open and closed loop conditions in the monkey. Exp Brain Res 14:318, 1972

37. Abel LA, Schmidt D, Dell'Osso LF, et al: Saccadic system plasticity in humans. Ann Neurol 4:313, 1978

38. Meyer CH, Lasker AG, Robinson DA: The upper limit of human smooth pursuit velocity. Vision Res 25:561, 1985

39. Van Den Berg AV, Collewijn H: Human smooth pursuit: Effects of stimulus extent and of spatial and temporal constraints of the pursuit trajectory. Vision Res 26:1209, 1986

40. Yasui S, Young LR: Perceived visual motion as effective stimulus to pursuit eye movement system. Science 190:906, 1975

41. Yarbus AL: Eye movements and vision. New York: Plenum Press, 1967:1

42. Krauzlis RJ, Lisberger SG: A control systems model of smooth pursuit eye movements with realistic emergent properties. Neural Computation 1:116, 1989

43. Watamaniuk SNJ, Heinen SJ: Is the visual system's insensitivity to acceleration also evident in the smooth pursuit system? Invest Ophthalmol Vis Sci 36:S205, 1995

44. Pola J, Wyatt HJ: Target position and velocity: The stimuli for smooth pursuit eye movements. Vision Res 20:523, 1980

45. Pola J, Wyatt HJ: Active and passive smooth eye movements: Effects of stimulus size and location. Vision Res 25:1063, 1985

46. Wyatt HJ, Pola J: Smooth eye movements with step-ramp stimuli: The influence of attention and stimulus extent. Vision Res 27:1565, 1987

47. Pola J, Wyatt HJ: The perception of target motion during smooth pursuit eye movements in the open-loop condition: Characteristics of retinal and extraretinal signals. Vision Res 29:471, 1989

48. Pola J, Wyatt HJ: Offset dynamics of human smooth pursuit eye movements: Effects of target presence and subject attention. Vision Res 37:2579, 1997

49. Barnes GR, Asselman PT: The mechanism of prediction in human smooth pursuit eye movements. J Physiol 439:439, 1991

50. Barnes GR, Asselman PT: Pursuit of intermittently illuminated targets in the human. J Physiol 445:617, 1992

51. Barnes GR: Visual-vestibular interaction in the control of head and eye movement: The role of visual feedback and predictive mechanisms. Prog Neurobiol 41:435, 1993

52. Rubin AM, Young JH, Milne AC, et al: Vestibular-neck integration in the vestibular nuclei. Brain Res 96:99, 1975

53. Weber RB, Daroff RB: Corrective movements following refixation saccades: Type and control system analysis. Vision Res 12:467, 1972

54. Dell'Osso LF, Troost BT, Daroff RB: Macro square wave jerks. Neurology 25:975, 1975

55. Dell'Osso LF: A dual-mode model for the normal eye tracking system and the system with nystagmus. (Ph.D. Dissertation). In: Electrical Engineering (Biomedical. University of Wyoming, Laramie, 1968:1

56. Dell'Osso LF: A model for the horizontal tracking system of a subject with nystagmus. Proc 20th Ann Conf EMB 9:24.2, 1967

57. Dell'Osso LF: A dual-mode model for the normal eye tracking system and the system with nystagmus. IEEE Trans Biomed Engng BME 17:87, 1970

58. Enright JT: The remarkable saccades of asymmetrical vergence. Vision Res 32:2261, 1992

59. Collewijn H, Erkelens CJ, Pizlo Z, et al: Binocular gaze movements: Coordination of vergence and version. In Ygge Y, Lennerstrand G (eds): Eye movements in reading. Wenner-Gren International Series. Oxford: Elsevier Science, 1994:97

60. Erchul DM, Jacobs JB, Dell'Osso LF: Latent nystagmus fast-phase generation [ARVO Abstract]. Invest Ophthalmol Vis Sci 37:S277, 1996

61. Zee DS, Fitzgibbon EJ, Optican LM: Saccade-vergence interactions in humans. J Neurophysiol 68:1624, 1992

62. Averbuch-Heller L, Zivotofsky AZ, Remler BF, et al: Convergent-divergent pendular nystagmus: Possible role of the vergence system. Neurology 45:509, 1995

63. Averbuch-Heller L, Zivotofsky AZ, Das VE, et al: Investigations of the pathogenesis of acquired pendular nystagmus. Brain 118:369, 1995

64. Hung GK, Semmlow JL, Ciuffreda KJ: The near response: Modeling, instrumentation, and clinical applications. IEEE Trans Biomed Engng BME 31:910, 1984

65. St. Cyr GJ, Fender DH: The interplay of drifts an flicks in binocular fixation. Vision Res 9:245, 1969

66. Steinman RM, Haddad GM, Skavenski AA, et al: Miniature eye movement. Science 181:810, 1973

67. Doslak MJ, Dell'Osso LF, Daroff RB: A model of Alexander's law of vestibular nystagmus. Biol Cyber 34:181, 1979

68. Dell'Osso LF: Evidence suggesting individual ocular motor control of each eye (muscle). J Vestib Res 4:335, 1994

69. Abel LA, Dell'Osso LF, Schmidt D, et al: Myasthenia gravis: Analogue computer model. Exp Neurol 68:378, 1980

70. Dell'Osso LF, Jacobs JB: A robust, normal ocular motor system model with congenital nystagmus (CN) including braking and foveating saccades. In Sharpe JA (ed): Neuro-ophthalmology at the beginning of the new millennium. Englewood: Medimond Medical Publications, 2000:107

71. Dell'Osso LF, Jacobs JB: A robust, normal ocular motor system model with latent/manifest latent nystagmus (LMLN) and dual-mode fast phases. In SharpeJA (ed): Neuro-ophthalmology at the beginning of the new millennium. Englewood: Medimond Medical Publications, 2000:113

72. Dell'Osso LF, Jacobs JB: A normal ocular motor system model that simulates the dual-mode fast phases of latent/manifest latent nystagmus. Biological Cybernetics 85:459, 2001

73. Jacobs JB: An ocular motor system model that simulates congenital nystagmus, including braking and foveating saccades (Ph.D. Dissertation). In: Biomedical Engineering. Case Western Reserve University, Cleveland, 2001:1

74. Dell'Osso LF: A hypothetical fixation system capable of extending foveation in congenital nystagmus. J Neuro-Ophthalmol 22:185, 2002

75. Jacobs JB, Dell'Osso LF: A robust, normal ocular motor system model with latent/manifest latent nystagmus (LMLN) and dual-mode fast phases. In Kaminski HJ, Leigh RJ (eds): Neurobiology of eye movements. From molecules to behavior—Ann NY Acad Sci 956. New York: NYAS, 2002:604

76. Jacobs JB, Dell'Osso LF: A hypothetical fixation system capable of extending foveation in congenital nystagmus. In Kaminski HJ, Leigh RJ (eds): Neurobiology of eye movements. From molecules to behavior—Ann NY Acad Sci 956. New York: NYAS, 2002:608

77. Garbutt S, Dell'Osso LF, Jacobs JB: “Staircase” saccadic intrusions and transient yoking and neural integrator failures associated with cerebellar hypoplasia. p. ARVO Abstr 1968. Annual Meeting Abstract and Program Planner [on CD-ROM or accessed at www.arvo.org], 2003

78. Robinson DA: A method of measuring eye movement using a scleral search coil in a magnetic field. IEEE Trans Bio Med Electron BME 10:137, 1963

79. Frens MA, van der Geest JN: Scleral search coils influence saccade dynamics. J Neurophysiology 88:676, 2002

80. DiScenna AO, Das V, Zivotofsky AZ, et al: Evaluation of a video tracking device for measurement of horizontal and vertical eye rotations during locomotion. J Neurosci Methods 58:89, 1995