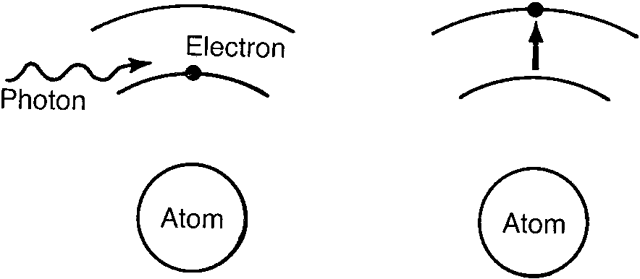
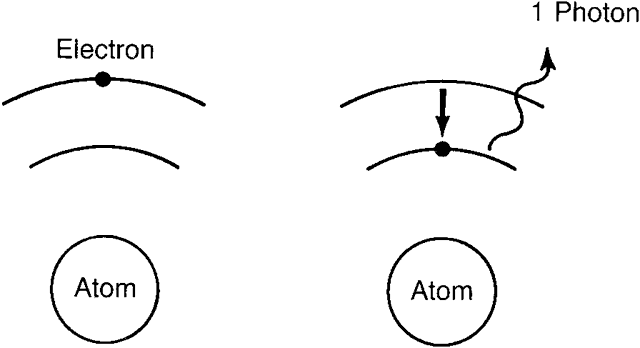
| Recently, it has become desirable to produce beams of even higher power
from solid-state lasers, such as the neodymium-YAG. Power increases like
this can be achieved by using the techniques of Q-switching or mode-locking. Q-SWITCHED LASERS Light from a pulsed solid-state laser, such as the ruby laser, does not
emerge as a single flash, but rather as a series of extremely brief ones. This
occurs because of the way the laser operates. For example, we
may consider the ruby laser, in which the population inversion is being
generated by a helical flash tube surrounding the ruby crystal. As
soon as enough excited electrons are present in the crystal, stimulated
emission occurs and the electrons are de-excited. The light from the
helical flash tube then re-excites the electrons, and another stimulated
emission (and laser flash) occurs. This continues for as long as
light from the flash tube is on, typically about a thousandth of a second. The “Q” in Q-switching is taken from the phrase quality factor, which is related to the ratio of energy storage to energy dissipation
in the laser medium. A laser with a high Q is storing energy well, whereas
one with a low Q is storing energy poorly. Q-switching is a method by which the Q factor of a laser apparatus can
be changed at a selected moment. It is a method to prevent laser action
from starting until a very large percentage of the electrons are in
the excited state. What Q-switching involves in theory is temporarily
to block one of the mirrors. Thus, no laser action can occur even though
electrons are being stimulated into their higher energy levels. When
the mirror is “unblocked,” reflection occurs and an enormous
amount of energy is released from the excited electrons present. The
duration of Q-switched pulses is of the order of 10 to 50 billionths (10-9) of
a second, termed nanoseconds. MODE-LOCKED LASERS Despite the theoretical purity of laser light, there are several factors
that may serve to contaminate it. In the operation of a high-power solid
laser, the output consists of a large number of waves of slightly
different wavelengths. One reason for this is that within a laser crystal many times larger than
the wavelength of light there is more than one wavelength that can
resonate back and forth. For laser operation, it is only necessary that
a whole number of wavelengths can fit in the space between the mirrors. For example, if
the length of the crystal is 10 m, then 100,000 waves of 100-μm
wavelength can “fit.” However, 99,999 waves of a fractionally
larger wavelength can also “fit,” and so on. Thus, multiple
resonant wavelengths are possible in a typical laser. A second reason for wavelength and/or resonance variability during the
use of a solid-state laser is that as the laser operates, the crystal
may become heated. This may result in a slight expansion, causing an increase
in the length of the rod and thus an increase in the distance
between the mirrors. Ordinarily, these different modes of oscillation operate independently, in
a situation known as a free-running mode. The large number of light waves with slightly different wavelengths, superimposed
with random phases, may result in a long train of light waves
with irregular amplitude. Mode-locking is a method of controlling these slightly differing modes
of emitted light. A layer of a suitable bleachable dye is placed in the
path of the beam within the laser cavity. This dye is opaque to the
light until the laser intensity builds sufficiently to saturate the dye
and to change it for a brief instant from opaque to transparent. During
that instant, the potential laser energy, which has been building
up in the meantime in a manner analogous to the energy buildup of the
Q-switched technique, is released. The phases of all the modes are thus “locked together,” resulting
in pulses in which all the modes combine to give a large resultant
power. The duration of these pulses is of the order of tens of trillionths (10–12) of
a second, termed picoseconds. These pulses are released as a series of half a dozen to a dozen short
pulses (a pulse train). The time between each pulse corresponds to the time it takes the light
to go back and forth between the mirrors in the laser cavity, typically
about 8 billionths (10-9) of a second. So, even though the distinction is made clinically between Q-switched and
mode-locked lasers, the mode-locked technique is actually a form of
Q-switching. Mode-locked and Q-switched lasers both have the common goal
of producing high-power laser pulses. Although the energy levels of
both types of lasers are approximately equal, the mode-locked laser
pulse lasts only about one one-thousandth as long as that from a Q-switched
laser. Since power is energy per unit time, the power of a mode-locked laser pulse is approximately one thousand times
greater than that of a Q-switched laser pulse. A Q-switched laser does not affect the relative phases of the components
of the laser light; it releases a single burst of laser energy. In contrast, a
mode-locked laser involves the additional feature of controlling
the phase of the emitted beam. The beam from a mode-locked laser
consists of a series of pulses, each pulse consisting of laser light
in identical phase alignment. In summary, mode-locking may be thought of as Q-switching plus phase-matching. Clinically, the output from a Q-switched laser consists
of a single pulse lasting from 10 to 50 nanoseconds (10-9 second). The
output of the mode-locked laser consists of a series of pulses, each 10 to 50 picoseconds (10–12 second) long; each series or train
of pulses may last 10 to 100 nanoseconds. DIODE LASERS All metallic elements are (at least fair) conductors of electricity. When
metallic atoms are close together, their outermost free electrons are
shared by all closely packed nuclei and are thus free to move in the
metal. When an electric field is applied to such a material, the electrons
feel an electrical “pressure,” or voltage. They move
and constitute an electrical current. If such a metal is heated, atomic
movement (electron-nucleus collisions) may be thought of as restricting
electron flow and the electrical resistance increases. Elements
that are electrical insulators have no such electrons free to roam in
the solid and thus do not conduct electricity. In between conductors and insulators is the class of elements known as
semiconductors. Typical examples are germanium and silicon. The outermost
orbits of these atoms contain four electrons. When large numbers of
these atoms are brought together, they can form a crystalline solid
in which each atom shares an electron with each of four nearest neighbors. At
low temperatures, there are no free electrons and these materials
do not conduct electricity. In contrast with conductors, however, as
these materials are heated, electrons may break free and begin to become
available to move under the influence of an electric field. Thus, (unlike
the situation with metals) as the semiconductor is heated, its
electrical resistance falls. When an electron in a semiconductor moves away from its atom, it leaves
behind a positively charged “hole” or vacancy. When an electric
charge is applied to such a material, the free (negatively charged) electrons
flow toward the positive terminal, and the (positively
charged) “holes” flow toward the negative one. (Actually the “holes” are
about three orders of magnitude heavier than
the electrons and thus move more slowly under any given voltage.) Electrons bound to their atoms usually are at their minimum possible energy
level. Then they are said to be in the valance band. If enough energy
is applied to these electrons, they may break free from their valence
bonds and become promoted into a higher energy band called the conduction
band. In the conduction band, these more energetic electrons
can roam and create an electric current. In a solid (unlike a gas), the atoms lie relatively close to each other, so
close that the presence of one atom's electron fields has an
effect on its neighbor's electrons. The electron energy levels become
disturbed and the material ends up with energy states that are “smeared” into
bands rather than discrete energy levels. In
an energy band, the energy levels are so close together that they are
in effect continuous. These valance and conduction energy bands of a semiconductor are separated
by a region of energy in which no allowed energy levels exist. This
region is called the forbidden region, and its width is called the band
gap. An electron in the conduction band has an energy greater than
an electron in the valence band by an amount equal to the band gap. If a large number of electrons is stimulated into the conduction band, it
leaves a corresponding large number of holes in the valence band. Now, let
us imagine that some photons strike these conduction band electrons. If
these photons have an energy equal to or slightly greater than
the band gap, they may cause the conduction electrons to drop back
into the valence band. As they do so, they release photons of this same
energy, which may then strike other stimulated electrons. It is easy
to see how this would result in coherent amplification. If this medium
is bracketed by a reflective surface at each end, laser output may be
produced in a manner analogous to the situation in gas lasers. This laser output is unlikely to occur in pure semiconductors because of
additional factors impeding electron transitioning such as crystal momentum, lattice
vibrations, and so forth. However, the behavior of these
semiconductor materials may be modified by adding impurities into
the structure. Adding some atoms of a different element is referred to
as doping. Arsenic, for example, has five electrons in its outer valence
shell. If we replace a semiconductor atom with arsenic, four of arsenic's
electrons are used for the crystal bonding. The fifth electron, conversely, is
relatively free to move in the crystal. Thus, addition
of a different element that contains five electrons in its outer
shell results in an excess of electrons, or negatively charged particles. Such
a semiconductor is called an n-type semiconductor. Similarly, if
we add an atom such as gallium, which has only three electrons in
its outermost shell, we create an excess of positively charged “holes.” Such
a conductor is called a p-type semiconductor. The increasingly ubiquitous (in ophthalmology) diode laser is created when
an n-type semiconductor is joined to a p-type semiconductor, forming
a p-n junction (Fig. 7). When this happens, electrons flow from the excess electron n-type side
to fill the holes in the excess hole p-type side (and it may be said
that the holes flow from the p-type side to the n-type side). Eventually, an
electric field is created that is strong enough to oppose any
further electron migration and the situation stabilizes. However, one
can stimulate this flow by connecting the n-type side to the negative
terminal of a source of direct current, and the p-type side to the positive
terminal. This causes further flow of electrons from the n-type
side (and further flow of holes from the p-type side). 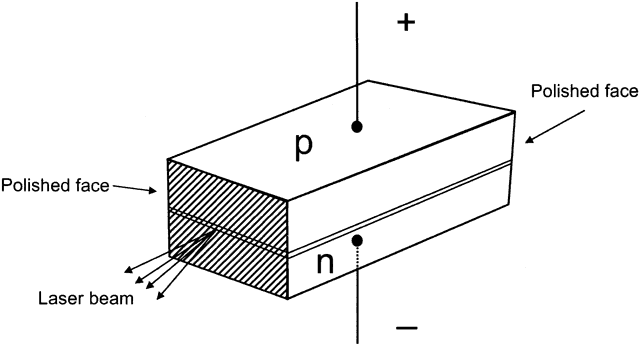 Fig. 7. Here, n-type and p-type semiconductors are joined at the junction. Negative
charge is applied to the n-type side, positive charge to the p-type
side. The back is mirrored and the front is partially mirrored to allow
laser emission. The sides are roughened to prevent laser emission
in other directions. Fig. 7. Here, n-type and p-type semiconductors are joined at the junction. Negative
charge is applied to the n-type side, positive charge to the p-type
side. The back is mirrored and the front is partially mirrored to allow
laser emission. The sides are roughened to prevent laser emission
in other directions.
|
These electrons and holes may then recombine (with what amounts to a transition
of the electrons back into the valence band and simultaneous
production of photons of the appropriate energy.) The produced photons
stimulate additional electron transitions back into the valence band (and
additional photon production). Under the influence of the voltage
applied to the p-n junction, electrons and holes are driven toward the
junction, where they combine to release photons. As the voltage (forward
bias) increases, more and more electrons from the n-type side and
more and more holes from the p-type side are driven toward the junction. The
increased number of electrons and “holes” combine
to produce an increased number of photons. Thus the emitted light intensity
becomes stronger. The region of the p-n junction where laser action
takes place is only a micron or so wide. One can design reflective surfaces at the ends of this “semiconductor
sandwich” by polishing the two faces of the crystal. The crystal-air
boundary provides a natural reflecting surface, and the natural
cleavage face of the crystal also makes an excellent mirror. A reflecting
surface at each end creates a resonant cavity, producing laser
emission. By varying the direct current, the laser output may be easily
modulated. Because emission results from transition between two energy
bands, rather than between two discrete energy levels as in a gas
laser, the emission is not quite so monochromatic as in a gas laser. The
wavelength is related to the energy difference between the valence
band and conduction band of that semiconductor. The diode laser is extremely small. Because of its direct conversion of
electricity into laser energy, it is highly efficient. The percentage
of photons obtained with respect to the number of electrons crossing
the junction is called the external quantum efficiency of the laser. It
varies with temperature, being of the order of 50% or more at the temperature
of liquid helium, for example, and still being about 15% at
room temperatures. In terms of the percentage of laser power output with
respect to the electrical power input, the efficiency can be as high
as 10%. Because the stimulated emission arises from within the host
material—and not from a small percentage of the active medium, as
in other lasers—the diode laser is by far the most powerful for
its size. FREQUENCY DOUBLING Many diode laser crystals have band gaps that correspond to wavelengths
in the infrared region. Diode lasers that emit in the infrared may have
limited clinical usefulness. Frequency doubling is a technique that
allows these lasers to produce laser radiation in a perhaps more clinically
desirable visible green, for example. Frequency doubling is possible
only because of the high power densities of lasers, and is due to
the manner in which light propagates through a solid medium. The nuclei
and electrons of solids form dipoles, which are stimulated to oscillate
and emit radiation themselves. Normally, the emitted radiation is
the same as the incident radiation. However, with very high power levels
nonlinear characteristics become significant. When this happens, oscillation
occurs not only at the incident frequency but at harmonics. The
strongest harmonic is at twice the incident frequency. With some
additional engineering maneuvers, this harmonic can be channeled as the
laser output. Solid state lasers that ordinarily “should” emit
only in the infrared can thus be altered into lasers that emit
in the visible green, for example. |