To achieve a large dynamic operational range, numerous adaptive changes take place within the visual pathway. The pupil controls, to a limited extent, the amount of light entering the eye. Two anatomically distinct retinae in the form of separate rod and cone photoreceptor systems are specialized for functioning in low or high ends of the operational range, respectively. Within the outer segment of the photoreceptor, the phototransduction cascade is regulated by background illumination level. The density of visual pigment within the outer segments of the photoreceptors is altered by background level and plays a significant role in determining sensitivity. Postreceptoral neural circuitry integrates and filters the output of the photoreceptors.

In general, all adaptation mechanisms reduce the response to light when background level is increased and, conversely, increase sensitivity when illumination is reduced. When background light level is low, the pupils dilate, the low threshold rod photoreceptors engage, and enhanced neural integration occurs across photoreceptors. At high background levels, pupillary constriction, activation of the cone photoreceptors, and reduced neural integration decrease the response to light. When adapted to low background levels, sensitivity is high, but with the cost of reduced spatial acuity and absent color vision. When adapted to high background levels, sensitivity to small changes in light is reduced with the benefit of increased spatial resolution and the ability to see color.

Impairment of adaptation mechanisms produces a loss of the ability to detect brightness differences (and hence the details of objects) under certain background light levels. The result is similar to the loss of image detail in an underexposed or overexposed photograph. An individual with congenital stationary night-blindness sees well in daylight but is unable to discriminate objects at twilight. Conversely, an individual with a cone dystrophy may be incapacitated by photophobia and poor acuity under daylight conditions, whereas vision in dim light is relatively unaffected. This chapter reviews the phenomenon of visual adaptation, its basic mechanisms, and its impairment in clinical disorders.

Once adapted to darkness, abrupt re-exposure to bright light results in a dazzling veil of brightness that also obliterates image detail. The dark-adapted visual system becomes highly sensitive to small changes in light. On stepping back outside from the theater, all light levels present in the image generate a maximal response, hence the differences in brightness needed to identify an object cannot be detected. After a much shorter time than for dark adaptation, sensitivity is adjusted, allowing perception of the brightness differences within the image.

Clinically, dark adaptation, or “bleaching” adaptation is the most frequency used method for assessing adaptation. Dark adaptation tracks the recovery of sensitivity in darkness following exposure to bright light, that is, a light sufficiently intense to convert the visual pigments to their bleached, or colorless form. Total dark adaptation is the state of highest sensitivity to light, which is attained only after about an hour in total darkness. Light adaptation refers to changes in visual system response properties as background illumination increases. As background illumination increases, color vision and spatial and temporal resolution improve dramatically; however, the threshold to detect faint lights becomes greatly elevated. The total dark-adapted eye is so sensitive that just several quanta can be reliably detected by a human observer.

PUPIL

The pupillary aperture provides the first stage of sensitivity regulation by regulating the amount of light entering the eye. Pupil diameter, although contributing to the optimization of vision when background light level is changed, is grossly insufficient to account for the range adaptation present in the visual system. When specifying the amount of light energy present in the retinal image, the troland (Td), a luminance unit weighted by the area stimulated is used:

(1)

Td = L × A

where L is luminance (in candelas per square meter, or cd × m^-2), and A is the area of the pupil (in square millimeters). Table 1 shows various useful relationships among luminance, retinal illuminance, pupil size, and visual function. Moving from complete darkness into bright light might cause the human pupil to constrict from 7 mm to 2 mm (Table 1). However, the ratio of the areas is less than 10 for these two pupil sizes. Hence, pupillary aperture can regulate the amount of light entering the eye only by about one log unit. This is grossly insufficient to account for the 14 log unit range of the visual system. In addition, it is apparent from Table 1 that above about 4.5 Td, the pupil has reached maximum constriction and thus can provide no additional regulation of light across the upper 4 log units of photopic luminance.

Several other observations of the pupillary response to light are of note. Pupillary response has a temporal course that does not precisely follow many documented psychophysical changes in sensitivity. Pupillary constriction begins about 200 msec after light onset and peaks at about 1 second.⁴ Complex changes in psychophysical thresholds occur within this time period⁵ (see section on temporal changes), implying the operation of adaptation mechanisms entirely independent of the pupil. In some instances, pupillary control mechanisms may actually impede adaptation. For example, following adaptation to high background levels, the pupil may remain constricted for some time after illumination decreases, during which time it can be shown that sensitivity continues to increase. Conversely, on entering a darkened area, the pupil dilates much faster than regeneration of visual pigment. Pupillary mechanisms enhance the light-gathering ability of the eye during the initial stages of dark adaptation, before the much slower biochemical changes within the photoreceptors begin to increase sensitivity. Thus, although the pupil makes important contributions to the adaptation process, regulation of the amount of light entering the eye provided accounts for only a small portion of the large dynamic range of the visual system.

DUPLEX RETINA

Duplex retinae contain separate, and largely independent, rod- and cone-mediated systems. These separate classes of photoreceptors are specialized for low and high levels of background lighting, respectively. The duplex retina thus greatly extends the operational range of the visual system. Table 1 shows the relationship between luminance in candelas per square meter (cd × m^-2) and retinal luminance (Td), across the functional range of the human visual system. The dimmest light levels (approximately the lowest 3 log units on the scale, from absolute threshold to cone thresholds) are responded to exclusively by the rod-mediated, or scotopic, system. The entire operational range of the rods (ending at rod saturation) spans 8 log units. The brightest light intensities (approximately the upper 5 log units, from rod saturation to an intensity where damage possible) are responded to exclusively by the cone-mediated, or photopic, system. The entire operational range of the cones is 11 log units. The region of overlap between the scotopic and photopic function is referred to as mesopic,⁶

How do these two classes of photoreceptor alter sensitivity with ambient light level? First, the clinician ought to note the different wavelength sensitivities of the two systems and the distribution of photoreceptors in the retina. The absorption spectra of the rods and the three cone types is shown in Figure 1. These psychophysically determined curves are in excellent agreement with the measured spectra of the photoreceptor pigments. The sensitivity of the human observer to scotopic and mixed-cone stimulation is shown in Figure 2.

At the most sensitive wavelength, around 510 nm, scotopic (rod) sensitivity is more than 1.5 log units more sensitive than the most sensitive photopic (cone) wavelength, approximately 530 nm (see Fig. 2). Understanding the effects of wavelength on sensitivity is necessary to predict sensitivity under dark-adapted conditions (see subsequent discussion).

The distribution of rods and cones varies considerably across the retina. Thus, the retinal location of the visual stimulus is critical for predicting the effects of adaptation. Figure 3 shows that the density of long- and medium-wavelength cones (sensitive to the red or green regions of the spectrum, respectively) drops off exponentially with distance from the fovea.⁷ Short-wavelength sensitive cones are distributed throughout the retina but spare the fovea. Rods are absent fovea, reach a peak density in the midperiphery, and greatly exceed cone density in the periphery. Therefore, both wavelength and retinal location of the stimulus are important factors in determining sensitivity to light and the state of adaptation. Clinical studies of dark adaptation typically present test stimuli at the 10 to 20 degrees eccentric to the fovea. At this eccentricity, rod density is at a maximum so that dark-adapted sensitivity may be measured at low backgrounds. However, cones are still plentiful at this distance from the fovea, thus assessment of cone sensitivity is not precluded at this eccentricity (see Fig. 3).

In animals with a different proportion of rods and cones than in humans, the scotopic and photopic ranges may be altered. For example, the cat has a rod/cone ratio approximately 100 times greater than humans and its rod system responds over the lower five log units of background levels whereas its cone system subserves adaptation over the upper three log units.²

Pigments

Photosensitive pigments consist of an opsin protein bound to the chromophore, retinal, which is derived from Vitamin A. There are four major visual pigments, one for the rods and one for each of the cone types: short-wavelength sensitive, medium-wavelength sensitive, and long-wavelength sensitive. Photopigment molecules are embedded in discs that make up the outer segment of the photoreceptor. There are approximately 1000 discs per rod photoreceptor. Each rod disc membrane can incorporate about 10,000 molecules of rhodopsin. Thus, there are about 10¹⁵ rhodopsin molecules in an eye, affording tremendous light-gathering capacity. One molecule of rhodopsin can be bleached by only one quantum of light. Once in the bleached, or transparent state, the molecule cannot capture any additional photons until it has regenerated. Bleached rhodopsin has a half-life of 5 minutes. Thus a 50% chance exists that a bleached rhodopsin molecule will have returned to the unbleached state at the end of a 5-minute interval. The depletion of photopigment by increased background level of illumination directly decreases system sensitivity. Although photopigment density is a significant factor in determining sensitivity changes across the operational range of the visual system, its role, particularly in the rod system is much smaller than originally thought (see section on mechanisms).

PHOTOTRANSDUCTION CASCADE

Light activation of visual pigment molecules located in the outer segments of the photoreceptors initiates a series of enzymatically catalyzed events that lead to the generation of a graded potential in the photoreceptors and eventually to an action potential in the optic nerve. The basic stages in phototransduction have been reviewed extensively.^8–10 Briefly, absorption of a photon of light transforms rhodopsin, the purplish visual pigment of the rods, from its 11-cis form to a colorless, or “bleached,”all-trans form. The change in the pigment characteristics result from conformational changes in the opsin molecule on absorption of a quanta. Light-activated rhodopsin interacts with the G-protein, transducin, causing the release of guanosine diphosphate and binding to guanosine triphosphate. Transducin-bound GTP then activates cyclic guanosine monophosphate (cGMP) phosphodiesterase (PDE) resulting in the hydrolysis of cGMP to 5'-GMP. A decrease in cGMP levels caused by PDE activation results in closure of membrane channels thus decreasing the otherwise continuous inward flow of Na⁺ and Ca²⁺ ions that takes place when the photoreceptor is in the dark. The gating of the “dark current” by light produces a graded hyperpolarization of the photoreceptor. Once initiated, the reaction must be quenched. This is accomplished at least partly through the actions of rhodopsin kinase and arrestin. The hyperpolarized photoreceptor cell membrane influences second-order neurons (bipolar cells) by controlling release of the neurotransmitter glutamate from the synaptic terminal of the photoreceptor. The graded release of glutamate results in either a hyperpolarization or depolarization of the postsynaptic neuron, depending on whether the synapse is sign preserving or sign inverting.¹⁰ Although homologous mechanisms are believed to exist for cone transduction, they have been studied less extensively.

The relationship between the illuminant and the light reflected from an object can be expressed as:

(2)

L = ρ(x,y) × E,

where L, the luminance variation in a scene, is the product of E, the intensity of the of the local illuminant, and ρ(x,y), which describes the reflectivities of the objects under view. That the relationship is multiplicative means that the contrast of illuminated objects is independent of the illuminant. Luminance contrast is defined as the difference between the maximum (Lmax) and minimum (Lmin) luminance weighted by their sum:

(3)

C = (Lmax - Lmin)/(Lmax + Lmin)

Applying this to the reflectivities [ρ(x,y)], of an illuminated object, we see that the contrast between any two points in the image is constant and thus independent of changes in the intensity of the illuminant, E.

140Ý

(4)

(ρ(x_i,y_i) × Eρ(x_j,y_i) × E)/(ρ(x_i,y_i) × E + ρ(×_j,y_i) × E)= (ρ(x_i,y_i)- ρ(x_j,y_i))/(ρ(x_i,y_i) + ρ(×_j,y_i))216Ý

The contrast, or the ratio between the luminance of any two points in the image, remains constant when illumination level is changed. This illustrates that a change in illumination levels, for example, a cloud drifting in front of the sun, or putting on sunglasses, does not alter retinal image contrast. For example, if A = 8 × 10⁵ Td, B = 2 × 10⁵ Td, the contrast would be (A-B) ÷ (B + A) = 0.6. If a dark cloud reduces the illuminant by a factor of 10,000, that is, C = 8 and D = 2, (C-D) ÷ (C + D) = 0.6. these relationships hold only for reflected light. If light is added to patterns displayed on self-luminous objects, such as a computer monitor's screen, contrast decreases until the difference in light levels fall below the threshold for detection, at which point the pattern is no be longer visible.

Clearly, most useful information present in an image is in the form of contrast. Thus, an ideal visual system should extract information from the reflected light ρ(x,y) × E completely independent of E, the illuminant.³ As noted, the visual system approaches this ideal by adjusting its sensitivity to vary inversely with E. When the visual system adjusts sensitivity proportionately with background level it is said to follow Weber's law (sometimes referred to as Weber fraction, or the Weber-Fechner relation). The visual system follows Weber's law when the slope of the smallest detectable increment (ΔI) is constant (K) across background level (I) such as

(5)

ΔI/I = K

When average background luminance is low, the visual system is highly sensitive to small differences within ρ(x,y). When background luminance is high, a larger change in luminance is required for detection.

Weber's law's function can be thought of as a kind of “automatic gain control.” A type of automatic gain control circuitry is built into devices such as radio and television sets to keep the output of the set constant when the transmitted signal weakens or wavers. In the visual system, the gain, or amplification of small changes in light, is large when background is low and small when the background is high. Rushton¹¹ proposed that a gain, or amplification stage early in the visual pathway could be regulated by a negative feedback signal, the strength of which is proportionate to the background level. The existence of a feedback signal would thus serve to optimize sensitivity of the system as background changed. Models of this type are generally of the form:

(6)

R/Rmax = I/I + σ

where the output (response, R, normalized to the maximum, Rmax) divided by itself plus a semisaturation constant, σ, the half-maximal response. The output of this system moves to an equilibrium over time preserving the response to a rapid change in input. It can be shown that these kinds of feedback gain-control models can accurately predict Weber-Law behavior under various conditions (for details, see earlier studies^2,12–15).

An adaptation mechanism placed early in the visual pathway allows finer changes in brightness to be encoded by the limited firing rate of the optic nerve. Without adaptation gain control mechanisms, a ganglion cell must convert the eight log units of luminance (action potentials per second) into unique firing rates.¹⁶ This would either vastly exceed physiologic limits for the ganglion cell firing rate, or result in only gross changes in contrast being signaled. A gain control mechanism placed early in the visual pathways preserves the full capacity of rate-limited neural elements to signal variations in luminance around the current average background level and thereby avoid saturation. The visual system is not unique in this arrangement. Weber's law relationships between background level and sensitivity occur early in the other sensory pathways, including the auditory, somatosensory, thermosensory, and chemosensory systems.

The precise nature of the feedback signal remains poorly understood. Horizontal cells have been considered likely candidates.¹⁷ However, although anatomically well-situated, their physiologic properties do not appear to be consistent with a gain control mechanism.¹⁸

The photoreceptors show electrophysiologic evidence of modulating their response with background level. Published evidence suggests that the drop in calcium within a rod after light exposure due to the closure of plasma membrane channels that prevent the influx of calcium while an active pumping mechanism involving sodium and potassium and calcium rapidly remove it.^10,19 The effect of calcium on phototransduction is now known to be indirect through interactions with binding proteins that play a role in recovery of the resting levels of cGMP after a flash of light and the dampening of multiple cycles of transducin activation following photoactivation of rhodopsin. These mechanisms serve the roles of amplification, or gain, and regulation.

INCREMENT THRESHOLDS

In this section, methods for studying light adaptation experimentally and their implications for clinical testing are considered. The classic psychophysical method for studying light adaptation and Weber's law is based on increment thresholds. The general psychophysical procedure in these tasks requires an observer to detect a small test flash that is briefly superimposed on a uniform background field of intensity, I. Psychophysically measured increment thresholds are derived from a plot of the percentage of correct detections for a range different intensities of the test flash. Threshold is defined as the point at which detection exceeds chance expectations (various curve-fitting and error estimation procedures are available to improve the accuracy of threshold calculation). These experiments can yield highly reliable data and have been used to investigate how sensitivity changes with background, eccentricity, wavelength, and other variables.

Figure 4 shows the increment thresholds to detect a spot of light superimposed on a uniform field of different levels. In this type of experiment, the uniform adaptation field had been viewed by the observer for a sufficient number of minutes to ensure that threshold measurements were consistent, that is, a stable adaptation level was reached. Thresholds are plotted for a wide range of background luminance levels and for two retinal eccentricities. In Figure 4, luminance units I, are weighted by the pupil area. This unit of luminance, the troland, is defined in the section on pupillary adaptation mechanisms. Note that there are several distinct segments to this curve. At very low levels of background illumination, the just-detectable luminance of the test flash on the background is a constant, that is, ΔI = K, and therefore does not follow Weber's law. Moreover, when background luminance is low, sensitivity is greater at the 7-degree eccentricity than when tested closer to the fovea. This is explained by the greater proportion of the highly sensitive rod versus cone photoreceptors at this distance from the fovea.

The lower portion of the increment sensitivity curve, up to about -3 log Td for the 7-degree eccentric test in Figure 4, illustrates what Barlow²⁰ termed “dark light.” In this range, the influence of the background light is negligible relative to the level of internal noise in the system. Potential sources of internal noise include random isomerizations of the photopigment molecules, spontaneous activity in outer segment membrane channels, and spontaneous neurotransmitter release. These internal events produce a sensation of light even in the complete absence of a background, often referred to as eigengrau, or “internal light”. This can be appreciated by carefully noting that, even in total darkness, the sensation of light is not entirely extinguished. Figure 4 also shows that whether there is no background (leftmost point), or whether the background light is less than 2 × 10^-3 Td, threshold does not change. On the basis of this type of experiment, Barlow²¹ calculated that the “dark light” at absolute threshold is equivalent to about 1000 quanta/sec^-1 delivered to the cornea, which after taking temporal differences and thresholds into account, predicts observed absolute threshold values of 100 quanta at the cornea.² (After correcting for losses due to media and the probability a photon will be absorbed by a pigment molecule, it is estimated that absolute threshold requires absorption of approximately 6 quanta.)

In Figure 4 threshold begins to rise at a background level of about -3 log Td for the 7-degree eccentric test. As background level exceeds the eigengrau, threshold begins to rise. Before attaining behavior according to the tenets of Weber's law, there is a transition zone, during which threshold rises with the square root of the background. This is referred to as the DeVries-Rose law portion of the light adaptation curve. Rose²² suggested that a slope following a square root law implied that threshold was limited by the quantal fluctuations that are inherent in any light source and limit sensitivity at these low background light levels. These relationships are shown in greater detail for the scotopic portion of the increment sensitivity curve in Figure 5.

This portions of the increment threshold curve labeled “dark light” and quantum fluctuations are regions where visibility is limited by internal or external noise, so that gain-control mechanisms are not yet operational. As background level increases, the threshold response of the rod system attains a constant slope and follows Weber's law. Thus, knowing the dark light level and the Weber fraction for a given experimental condition enables prediction of the rod increment threshold across the entire scotopic range. An example is a model used by Lamb²³:

(7)

ΔI/ΔI₀ = (1 + I/I_D)n

where ΔI₀ is the threshold in the absence of a background (absolute threshold), I_D is the constant level corresponding to the dark light level, and n is an exponent that describes the slope of the increment threshold curve. When n is close to 1, the system approaches ideal behavior according to Weber's law. That is, when n = 1, there is a perfect cancellation of the effect of the illuminant, E. Depending on the conditions of the increment sensitivity experiment, empirical estimates of n vary between 0.7 and 1.0.

Figure 4 shows that between backgrounds of about -1 and 0 log Td, the curve again flattens. This region is a transition zone between rod and cone function. Above about -1 log Td, the rods “saturate,” that is, further increments in luminance produce no additional rod-generated activity because their response is already maximal. This is indicated by the vertical line at the right-most portion of Figure 5, implying infinite threshold for the rod system above these background levels. The flattened portion of the curve in the middle of the graph represents a form of dark light behavior for the cone system. At this stage, the rods are saturated but the cone system is not sufficiently stimulated to detect a change from the “cone eigengrau.” At higher levels of background luminance, cone function begins to dominate and the curve again attains a constant slope and Weber's law behavior that holds for at least additional 3 log units of background. At very high levels of background (not shown in Fig. 4), cones also saturate. Cone saturation is difficult to demonstrate experimentally and typically requires very brief test flashes. Cone saturation is avoided at least partly due to pigment depletion by the background.

RELATIONSHIP TO PERIMETRY

Clinically, increment threshold sensitivity forms the basis for standardized perimetry. Static perimetry is used to determine the threshold for detecting small spots of light projected at fixed locations on a diffusely lighted background. The purpose of such testing is to reveal the retinal locations of functional loss. Thus the test spot in perimetry is analogous to ΔI and the background light, I. At low levels of I, foveal threshold is relatively elevated because of the paucity of rods at this location in the retina. At higher background levels, the cone system begins to dominate and threshold is relatively decreased (i.e., sensitivity is increased) in the foveal region. The relationship between eccentricity, relative thresholds, and absolute background levels in perimetry is illustrated in Figure 6.²⁴

Most modern perimetry systems uses a background level of 10 candelas/m² (corresponding to 31.5 apostilbs [another measure of luminance] as used in Fig. 6). This background level is similar to the lighting levels in offices, and thus adaptation time for the patient is minimized. In addition, because the cone system remains active at these background levels, clinical perimetry reveals the classic “hill of vision” and thus has the advantage of assessing foveal function. If the background luminance was set in the scotopic range, and the observer sufficiently dark adapted, instead of the hill of vision centered at the fovea, a relative scotoma appears. Aulhorn's curves of vision²⁴ illustrate the inversion of sensitivity at the fovea under photopic and scotopic adaptation conditions (see Fig. 6).

SPATIAL INFLUENCES ON LIGHT ADAPTATION

The classic increment sensitivity experiments described above typically employed a sharp-edged spot and a uniform background as stimuli. The principles of light adaptation derived from these experiments do not fully take into account spatial and temporal variations in the stimuli. One of the more striking illustrations of spatial interactions in adaptation are the familiar Mach bands (Fig. 7A).

The stimulus arrangement that reveals these effects is typically a series of uniform gray patches that differ in brightness. At the border of a uniform light and dark patch, a band of relative lightness appears on the lighter patch and a band of relative darkness appears on the darker patch. Clearly, the adaptation level induced by one patch affects sensitivity at a spatially distant location. Thus some aspects of adaptation are not strictly “local,” that is, confined to a single neuron. The appearance of Mach bands is thought to reflect the operation of lateral inhibition, an important method for enhancing image contrast by post-receptoral neurons. Similar interactions between spatial configurations and light sensitivity are apparent in the “scintillating grid” (see Fig. 7B).

A large body of psychophysical and electrophysiologic data shows that the postreceptoral visual system is organized as receptive fields, with spatially distinct regions of excitation and inhibition. When sinewave gratings of different spatial frequencies (i.e., the reciprocal of stripe width) are used in increment threshold tasks, the relationship between threshold and background luminance deviates significantly from the form the of curve illustrated in Figure 4. Figure 8²⁵ shows the effect of light adaptation on threshold to detect the contrast of gratings of various spatial frequencies. At high luminance levels, the human visual system acts as a band-pass filter: sensitivity is greatest at medium (3 to 5 cycles per degree [cpd]) spatial frequencies and then drops off precipitously at high and low spatial frequencies. At low luminances, the human visual system's low spatial frequencies are no longer attenuated. Clearly, background adaptation level interacts with sensitivity to the spatial features in a image in a complex and nonlinear fashion.

These data also illustrate the dramatic increase in acuity (in this case grating resolution) with background luminance. At 9 × 10² Td average luminance, acuity approaches 48 cpd compared with an average luminance 9 × 10^-3 Td, where acuity drops to 4.8 cpd. Because spatial frequency-tuned units arise only in postreceptoral neural units, these findings point to an important role for higher-level neuronal processes the control of sensitivity.²

CONTRAST ADAPTATION

If a high contrast grating is viewed for several minutes, the minimum contrast needed to detect the grating (contrast threshold) is significantly elevated, provided the test gratings are of similar spatial frequency and orientation.²⁶ Neurophysiologic evidence indicates that neurons from the ganglion cell level through primary visual cortex adjust their gain as a function of the background contrast.^27,28 Contrast adaptation effects have been used extensively to study the spatial frequency and orientation tuning properties of spatial vision mechanisms and are beyond the scope of this chapter. Following logic similar to that used in the discussion of light adaptation, contrast adaptation may be thought of as enhancing discrimination of high-contrast objects on highcontrast backgrounds.

TEMPORAL FREQUENCY DEPENDENCE OF ADAPTATION EFFECTS

How rapidly can the visual system alter its sensitivity following an increase in background illumination? Experiments by Crawford⁵ addressed this question by examining sensitivity to a test flash at varying intervals from the onset of a background conditioning flash.

Figure 9 illustrates rapid changes in sensitivity produced by a 500-msec conditioning flash of differing intensities. When a brief test flash is coincident with the onset of the conditioning flash, threshold is elevated by as much as 4.5 log units and then declines to a plateau within about 50 msec. Following offset of the 500-msec conditioning flash, threshold declines rapidly, decreasing 2.5 log units within 100 msec. The somewhat confusing rise in threshold prior to the onset of the conditioning flash results from “backward masking” and is attributed to neural delay for the dim test flash relative to the conditioning flash: the inverse relationship between latency and intensity is thought to allow the onset of the bright background to create an effective “neural background” before the test flash arrives at higher perceptual centers (even though the test flash preceded the background increment). The effective neural background increase at the time of test stimulation thus results in an elevation of threshold.

Background luminance also greatly affects perception of movement, or flicker. When a sinusoidal grating is temporally modulated (the light and dark bars are exchanged at a fixed rate in time), and the just-detectable contrast is determined for different average luminance values, Weber's law obtains only when temporal frequency is low or spatial frequency is low.²⁹ High spatial frequencies (fine gratings), and moderate temporal frequencies produce marked departures from Weber's law (Fig. 10). These results suggest that adaptation mechanisms are rather slow to engage and lose effectiveness above 8 Hz. At high temporal and low spatial frequencies, detection is relatively unaffected by adaptation level.² These results are consistent with studies of photoreceptor kinetics, which show that, unlike rods, the rising phase of the cone photocurrent is unaffected by background.²³

Eye Movements

The eye is continually in motion, even during apparently steady fixation. Although the eye subjectively appears to maintain foveation of a target in a steady and unvarying fashion, accurate measurements reveal the presence of small slowly drifting movements together with rapid “microsaccades.”³⁰ These small eye movements cause the retinal image to dance across the receptor mosaic continually, effectively introducing temporal modulation into any freely viewed image. If retinal image movement is eliminated by specialized apparatus that effectively removes all temporal modulation in the retinal image, the perceived image fades and eventually disappears.^31,32 Abrupt termination of image stabilization causes the faded image to reappear quickly, much faster than could be accounted for by the slow pigment regeneration mechanisms. Fading of stabilized retinal images probably explains why retinal vessels normally are not visible but may appear when, for example, during a slit-lamp examination, the vessels are illuminated from a different angle and stimulate an unadapted portion of the retina. Image fading under stabilized viewing is another phenomenon that is not easily explained by photoreceptor pigment bleaching. The abrupt addition of uniform light to a faded stabilized image results in a paradoxical after-image.¹³ Furthermore, the rapidity of these nonlinear effects implies engagement of postreceptoral neural processes. Image fading can be demonstrated without special equipment if a dim patch of light, especially one with blurred edges, is viewed in the periphery. After several seconds of steady fixation, the eccentric patch of diffuse light fades from sight. This type of fading is referred to as Troxler's phenomenon.

If the pre-exposure light is sufficiently intense to deactivate the rod system, the area of the retina tested is in the midperiphery, and the test wavelength is appropriate for rods, then a characteristic two-limbed function is obtained. Figure 12 shows classic dark adaptation curves obtained after pre-exposure to five intensities of light.³⁶ When the adapting light was 4 × 10⁵ Td, threshold drops about 1 log unit in the first few minutes. Threshold then changes only slightly until about 10 minutes of dark adaptation have elapsed, at which time a second exponential decline in threshold begins. Threshold then declines about 2 additional log units, reaching maximal sensitivity only after 35 to 40 minutes in total darkness.

Numerous experimental manipulations indicate that the initial portion of the biphasic dark adaptation curve reflects cone sensitivity whereas the second portion reflects recovery of rod sensitivity. If the prior adapting light is very weak, threshold declines more rapidly, without the scalloped break near 10 minutes after adaptation (see Fig. 12).³⁷ This is because the rods are not significantly depleted of their photopigment by a weak adapting light, thus recovery of high sensitivity occurs more rapidly. Similarly, if the adapting light, however intense, is so brief that rod pigment is not depleted the scalloped portion of the curve is likewise absent. Conversely, as expected based on the duplex nature of the retina, if the wavelength of the test light is long, that is in the red region of the spectrum such that only L-cones are stimulated, the late-phase decrease in threshold fails to occur. Under these conditions threshold remains elevated at the level of the rod-cone break that normally occurs 10 minutes into dark adaptation (Fig. 13). Indeed, by testing with different wavelengths of light, it can be shown that the spectral sensitivity of the lower portion of the adaptation curve is in agreement with the scotopic luminous efficiency curve (λ') and the spectral sensitivity of the upper portion of the curve corresponds to photopic luminous efficiency (λ). In addition, as predicted from duplex theory, dark adaptation threshold fails to decline from the cone asymptotic level if the test light is small and centered on the fovea (see Fig. 11).

LIGHT ADAPTATION

For many years, the photochemical theory was assumed to provide the basis of scotopic sensitivity changes with background level, although the original proponents of the theory, Hecht and coworkers,³⁸ readily recognized its limitations. According to the photochemical theory, a 50% bleach should elevate the rod threshold by a factor of 2. In fact, a 50% bleach raises threshold by 10 log units (10¹⁰). With the advent of the technique of reflection densitometry, this finding was demonstrated empirically. Reflection densitometry measures the proportion of pigment bleached in the living eye by comparing radiometric measures of light reflected by the fundus before and after exposure to the bleach of any given wavelength. Pigment density is proportional to the difference in the amount of light reflected from the fundus under the two conditions. The relationship between the ability to detect light and the proportion of bleached pigment is described by the Dowling-Rushton equation^39,40:

(8)

log(ΔI/ΔI₀) = kP

where k is a constant and P is the proportion of bleached pigment. Various experiments indicate the approximate value of k for rods and for cones is 20 and 3, respectively. Thus, for a given proportion of bleached pigment, there is a faster rise in threshold with background level for the scotopic (rod) versus the photopic (cone) system. As noted, rods saturate (i.e., there is no additional response regardless of the size of the increment) far below the point at which complete pigment bleaching occurs. However, the cones maintain behavior in keeping with Weber's law beyond the point of 100% bleaching of cone pigment (Fig. 14). With cones, pigment depletion plays a significant role in upholding Weber's law. Bleaching of pigment effectively reduces the light stimulus to the cones and hence photopic threshold continues to rise proportionately with background, extending the Weber region into luminance levels (6 × 10⁶ Td) that bleach virtually all of the cones.^6,41

NEURAL ADAPTATION

Convergence, or spatial summation, in the rod system was suggested by Rushton⁴² as part of the explanation for the discrepancy between rod sensitivity and pigment bleaching. Rushton showed that only a few rods need to absorb a photon to significantly elevate threshold across a wide area.⁴³ At background levels that stimulate only 1 rod in 50, threshold in the unstimulated rods is elevated by a factor of 4. This lateral spread of adaptation in the scotopic system is thought to be mediated by a neural adaptation pool, in which many rods feed into a single bipolar cell, effectively amplifying light by summing many small hyperpolarizing events. Cones do not manifest convergence extensively onto bipolar cells and therefore they are less subject to the effects of spatial summation. Thus, neural circuitry early in the visual pathway plays an important role in adaptive processes.

EQUIVALENT BACKGROUND

Reflection densitometry measurements have shown that the slow recovery of psychophysical threshold during dark adaptation is accounted for by the time course for the bleaching and regeneration of visual pigments. Early work by Crawford^5,44 and by Rushton and Powell³⁷ demonstrated that, after different amounts of bleaching light, dark adaptation thresholds followed the family of exponential curves predicted in Equation 4. Inasmuch as the probability is 0.50 that a bleached rhodopsin molecule will revert to the unbleached state within 5 minutes, it can be expected that 50% of the bleached rhodopsin will be recovered within this time period.⁴² Figure 15 shows the equivalent background experiment of Blakemore and Rushton.⁴⁵ The data are from an individual with achromatopia and thus uncontaminated by cone function across a wide range of backgrounds. Two sizes of test flash were used to produce different thresholds. The larger target has a lower threshold due to spatial summation. The equivalent background at a given point during dark adaptation is determined by drawing a horizontal line to the corresponding point on the increment threshold graph on the right until it intersects the threshold line and then reading the corresponding background. The thresholds for the two flashes are elevated the same relative amounts. This method of determining the equivalent background is independent of the size or duration of the test flash. Thus, there appears to be a common mechanism that regulates rod sensitivity in both dark and light adaptation. In other words, postreceptoral neurons do not distinguish between the state of adaptation in the dark following a bleach and a real light background.

Adaptation may be similarly affected in individuals with cone dystrophies. These disorders typically have a later onset and are distinguished from macular dystrophies by the diffuse nature of cone involvement. Inheritance patterns include autosomal dominant, autosomal recessive, X-linked recessive with tapetal-like sheen, and X-linked rod-cone forms.⁴⁷ As with rod monochromacy, ERG to cone-isolating stimulus conditions is absent. Unlike rod monochromacy in which cones are congenitally absent, cone dystrophies often show an elevated and prolonged cone limb (i.e., the first 10 minutes) of the dark adaptation curve.

In contrast to disorders of cone-mediated vision, a complimentary set of symptoms is observed in disorders of the rod system. Congenital stationary night blindness (CSNB) is a term for a group of disorders with two major subtypes.⁴⁶ One group includes those with a normal-appearing fundus. This form of CSNB may have autosomal recessive, autosomal dominant, or X-linked recessive modes of transmission. CSNB with a normal-appearing fundi includes Nougaret and Schubert-Bornschein subtypes. The Nougaret form (Fig. 16) is characterized by a monophasic dark adaptation curve that typically asymptotes at or above the normal cone plateau. Photopic abnormalities may also be present in this disorder, manifesting as prolonged or elevated cone thresholds. Early studies by Carr and Gouras⁴⁸ using reflection densitometry showed that rod pigment was present in both subtypes of CSNB, implying a defect in transduction or transmission. Recent molecular studies have isolated at several mutations in genes controlling phototransduction associated with CSNB. Dryja and colleagues have shown that a missense mutation in the rhodopsin gene is associated with CSNB and speculated that this mutant opsin would continuously activate transducin, resulting in a rod dysfunction.⁴⁹ Other studies indicate that the Nougaret form of CSNB is associated with mutations in the gene encoding rod transducin⁵⁰ and is also characterized by constitutively active rods, that is, not from an absence of the rod response.⁵¹

The more common Schubert-Bornschein subtype of CSNB is further subdivided into complete (no dark adaptation) and incomplete (1 to 1.5 log unit elevation of final rod threshold) variants. An X-linked form is associated with high myopia and nystagmus.

The second group of CSNB disorders includes individuals with abnormal-appearing fundi. These disorders include Oguchi's disease, fundus albipunctatus, and the flecked retina of Kandori. The dark adaptation thresholds in these entities are characterized by greatly elevated and prolonged portions of the rod segment of the dark adaptation curve. In Oguchi's disease, normal rod threshold may be reached only after several hours in total darkness (Fig. 17).⁴⁸ Total dark adaptation may be accompanied by Mizuo's phenomenon, in which an unusual metallic sheen in the fundus disappears after several hours of dark adaptation. Recently, genetic studies have shown that a null mutation of the rhodopsin kinase gene, results in prolonged adaptation⁵² and is present in some patients diagnosed with the Oguchi form of CSNB.^53,54 Fundus albipunctatus has recently been associated with mutations in 11-cis retinol dehydrogenases, resulting in a delay in the regeneration of rod and cone pigments.⁵⁵

Retinitis pigmentosa (RP) is a hereditary progressive retinal degeneration with a prevalence of 1 in 4000⁵⁶ that occurs in autosomal dominant, autosomal recessive, and X-linked forms. Typically, RP begins as a rod-dominated loss resulting in progressive nyctalopia, loss of peripheral visual field, and abnormal dark adaptation. As the disease progresses, the cones and central vision also become involved. RP is associated with several mutations in the genes that encode proteins in rod phototransduction pathways, and thus the condition could be expected to affect night vision.⁵⁷ More than 70 mutations in the rhodopsin gene have been associated with various forms of RP and CSNB.⁵⁸

Abnormalities of rod-mediated night vision may also be associated with various systemic disorders, particularly those affecting vitamin A levels.⁵⁹ Vitamin A is stored in the liver and transported to the retinal pigment epithelium in the form of retinol, along with retinol binding protein, where it is converted to retinal through the action of zincdependent enzyme alcohol dehydrogenase.⁶⁰ Retinal combines with protein opsin to form rhodopsin. If the liver becomes exhausted of its stores of vitamin A, rhodopsin levels can become depleted, eventually impairing scotopic vision. Vitamin A-related nightblindness can be caused by malnutrition, intestinal malabsorption⁶⁰ such as in Crohn's disease, defects of fat metabolism, liver disease, biliary cirrhosis,⁶¹ cystic fibrosis,⁶² chronic alcoholism, and through urinary excretion in cancer and infections.⁵⁹ Dark adaptation curves are either greatly elevated or prolonged, depending on the severity of the deficiency. Dark adaptation testing may be used clinically to monitor recovery following Vitamin A therapy, which in some cases can result in complete recovery of rod function.⁶⁰ It may be necessary to verify blood levels of vitamin A following supplementation, particularly in cases of malabsorption. Figure 18 shows the the effect of Vitamin A therapy on the dark adaptation functions following different intensity bleaches in a patient with Crohn's disease and Vitamin A deficiency.⁶³ Pretherapy, a 100% bleach delayed the cone recovery time and the rod-cone break. At the end of 75 days of supplementation therapy, the patient's cone- and rod-recovery curves were within normal limits. The study of Cideciyan and associates suggests that the slowed dark adaptation reflects a limit on the rate of one of the regeneration processes in the visual cycle imposed by the unavailability of retinoid.⁶³

As a result of high metabolic demands, the retina is also susceptible to hypoxia.⁶⁴ Hypoxic conditions can affect thresholds as low as 9000 feet.⁵⁹ Coronary artery disease can have pronounced effects on dark adaptation,⁶⁵ which may be reversible after circulation has been restored.⁶⁶

The normal process of aging has been associated with several changes in dark adaptation. Early studies, notably those of McFarland and Fisher,⁶⁹ indicated a systematic decline in photopic and scotopic sensitivity during dark adaptation through age 60 years. Decreased foveal sensitivity during dark adaptation in older people has been associated with a slower rate of pigment regeneration in the same individuals.⁷⁰ More recent studies suggest that even when ocular pathology and the properties of the senscent lens are controlled for, scotopic sensitivity remains elevated in older individuals.⁷¹ These age-related differences in scotopic sensitivity are uniformly distributed in central and peripheral vision.^71,72

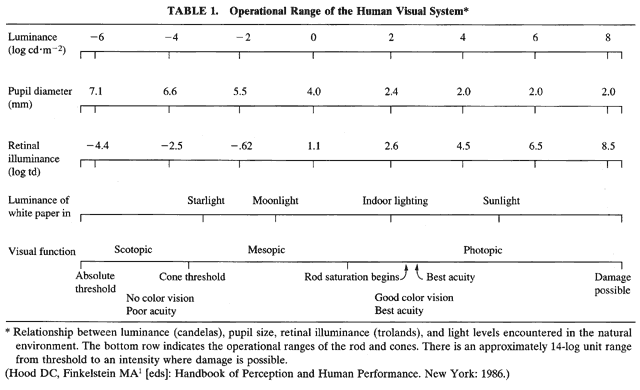
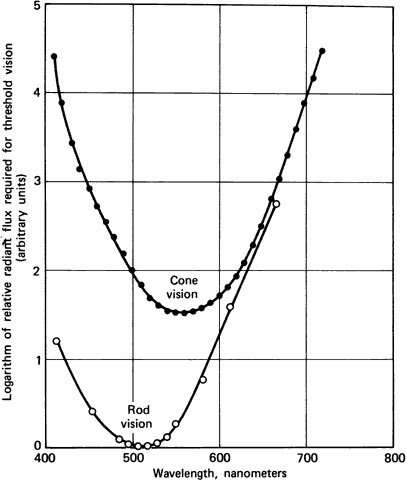
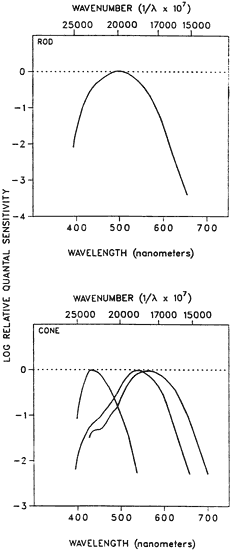
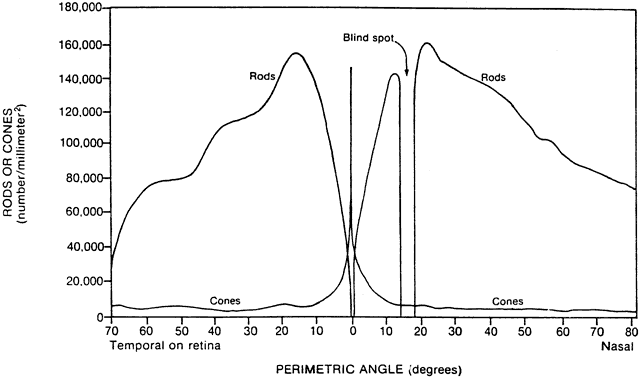
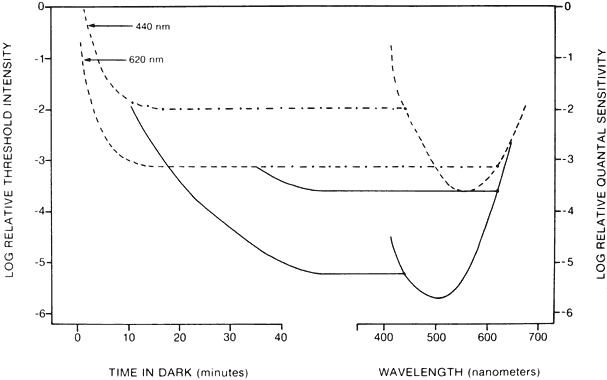
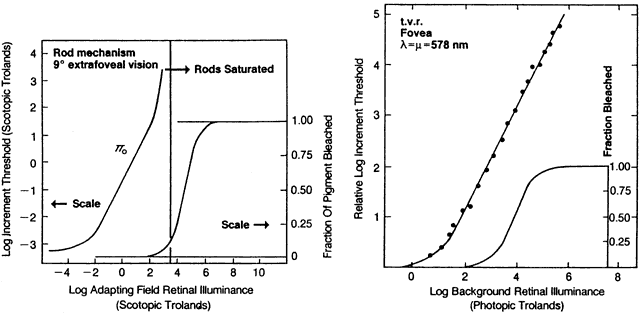
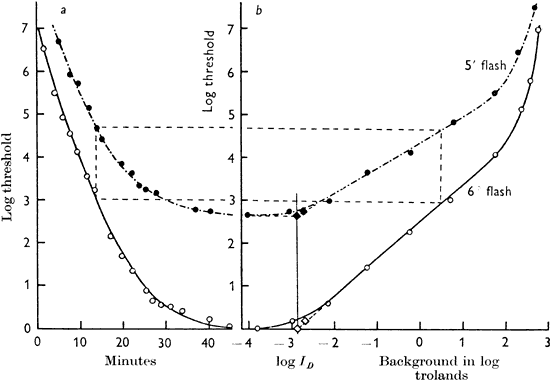
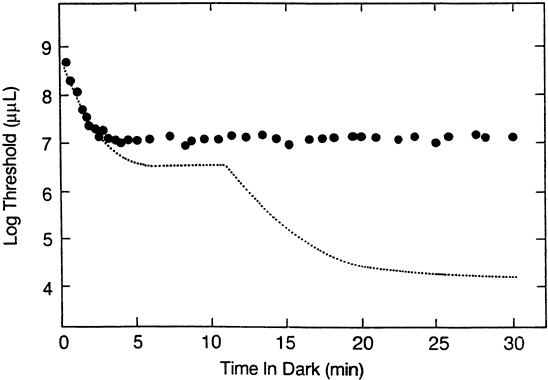
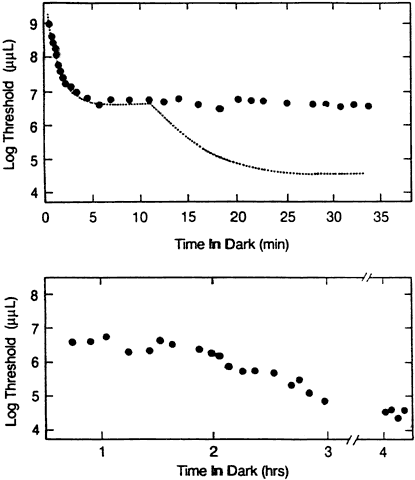
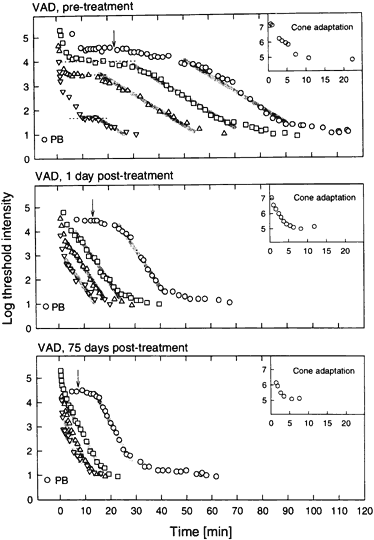
1. Hood DC, Finkelstein MA: Sensitivity to light. In Boff KR, Kaufman L, Thomas JP (eds): Handbook of Perception and Human Performance, pp 1–66. New York: Wiley, 1986

2. Shapley R, Enroth-Cugell C: Visual Adaptation and Retinal Gain Controls, pp 263–346. Oxford, UK: Pergamon, 1984

3. Green DG: Visual acuity, color vision, and adaptation. In Albert DM, Jacobiek FA (eds): Principles and Practices of Ophthalmology, pp 332–349. 1st ed. Philadelphia: WB Saunders, 1994

4. Loewenfeld IE: The Pupil. Ames, IA: Iowa State University Press, 1992

5. Crawford B: Visual adaptation in relation to brief conditioning stimuli. Proc R Soc Lond (Biol) 134:283, 1947

6. Pokorny J, Smith VC: Color vision and night vision. In Ogden TE (ed): Retina, pp 127–145. St Louis: Mosby, 1994

7. Osterberg G: Topography of the layer of rods and cones in the human retina. Acta Ophthalmol Suppl 6:1, 1935

8. McNaughton PA: Light response of the vertebrate photoreceptors. PhysiolRev 70:847, 1990

9. Stryer L: Molecular basis of visual excitation. Cold Spring Harbor Symp Quant Biol 53:283, 1988

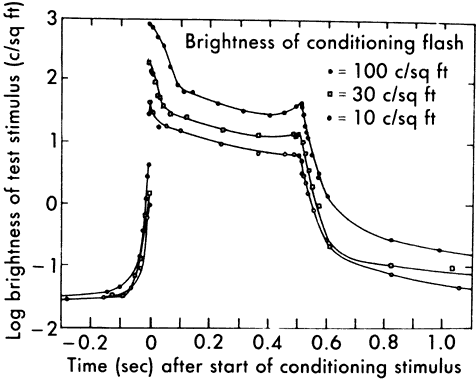
10. Yau K-W: The Friedenwald Lecture. Phototransduction mechanism in retinal rods and cones. Invest Ophthalmol Vis Sci 35:9, 1994

11. Rushton WAH: Bleached rhodopsin and visual adaptation. J Physiol 181:645, 1965

12. Hart WM: Visual adaptation. In Hart WM (ed): Adler's Physiology of the Eye, pp 502–530. St Louis: Mosby, 1992

13. Tulunay-Keesey U, Saleh G, Ver Hoeve JN et al: Apparent phase reversal during stabilzied image fading. J Opt Soc Am 4:2166, 1987

14. Hahn LW, Geisler WS: Adaptation mechanisms in spatial vision: I. Bleaches and backgrounds. Vision Res 35:1585, 1995

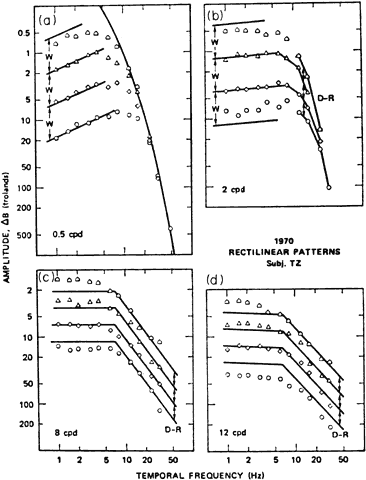
15. Kortum PT, Geisler WS: Adaptation mechanisms in spatial vision: II. Flash thresholds and background adaptation. Vision Res 35:1595, 1995

16. Barlow HB: Optic nerve impulses and Weber's Law. Cold Spring Harbor Symp Quant Biol 30:539, 1965

17. Dowling JE: The site of visual adaptation. Science 155: 273, 1967

18. Lankheet MJ, Rowe MH, van Wezel RJ et al: Horizontal cell sensitivity in the cat retina during prolonged dark adaptation. Vis Neurosci 13:885, 1996

19. Dizhoor A, Ray S, Kumar S et al: Recoverin: A calcium sensitive activator of retinal rod guanylate cyclase. Science 251:915, 1991

20. Barlow HB: Retinal noise and absolute threshold. J Opt Soc Am 46:634, 1956

21. Barlow HB: Increment threshold at low intensities considered as signal noise discriminations. J Physiol 136:469, 1957

22. Rose A: The sensitivity performance of the human eye on an absolute scale. J Opt Soc Am 38:196, 1948

23. Lamb TD: The role of photoreceptors in light-adaptation and dark-adaptation of the visual system. In Blakemore C (ed): Vision: Coding and efficiency, pp 161–168. Cambridge, UK: Cambridge University Press, 1990

24. Aulhorn E: Über die Bezeihung zwischen Lichtsinn und Sehasharfe. Graef's Arch Ophthalmol 167:4, 1964

25. Van Nes FL, Bouman MA: Spatial modulation transfer in the human eye. J Opt Soc Am 57:401, 1967

26. Blakemore C, Campbell FW: On the existence of neurones in the human visual system, selectively sensitive to the orientation and size of retinal images. J Physiol 203:237, 1969

27. Ohzawa I, Sclar G, Freeman RD: Contrast gain control in the cat's visual system. J Neurophysiol 54:651, 1985

28. Carandini M, Ferster D: A tonic hyperpolarization underlying contrast adaptation in cat visual cortex. Science 276: 949, 1997

29. Kelly DH: Adaptation effects on spatio-temporal sine-wave threshold. Vision Res 12:89, 1972

30. Ratliff F, Riggs LA: Involuntary motions of the eye during monocular fixation. J Exp Psychol 40:687, 1950

31. Ditchburn RW, Ginsborg BL: Vision with a stabilized image. Nature 170:36, 1952

32. Riggs LA, Ratliff F, Cornsweet JC et al: The disappearance of steadily fixated visual test objects. J Opt Soc Am 43: 495, 1953

33. Barlow HB, Sparrock JMB: The role of after-images in dark adaptation. Science 144:1309, 1964

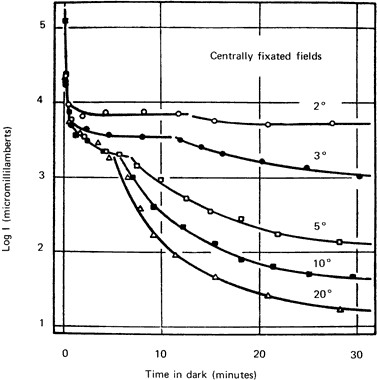
34. Jacobson DM, Thompson HS, Bartley JA: X-linked cone dystrophy: Clinical characteristics of affected male and female carriers. Ophthalmology 96:895, 1989

35. Kemp CM, Jacobson SG, Faulkner DJ et al: Visual function and rhodopsin levels in humans with vitamin A deficiency. Invest Ophthalmol Vis Sci 46:188, 1988

36. Hecht S, Haig C, Wald C: The dark adaptation of retinal fields of different size and location. J Gen Physiol 19:321, 1935

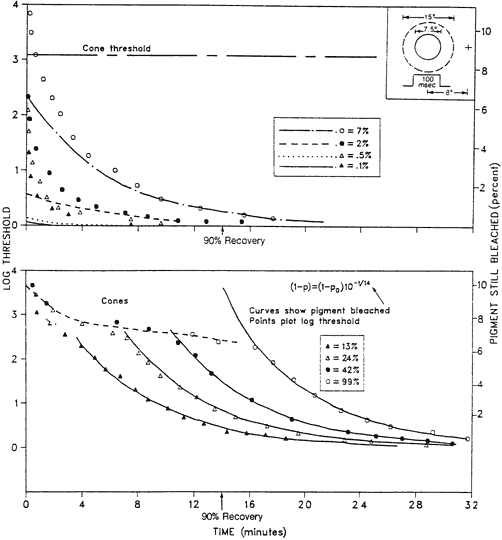
37. Rushton WAH, Powell DS. The rhodopsin content and the visual threshold of human rods. Vision Res 12:1073, 1972

38. Hecht S, Schlaer S, Pierenne MH: Energy, quanta, and vision. J Gen Physiol 25:819, 1942

39. Dowling JE: Chemistry of visual adaptation in the rat. Science 188:114, 1960

40. Rushton WAH: Rhodopsin measurement and dark adaptation in a subject deficient in cone vision. J Physiol 156: 193, 1961

41. Enoch JM: The two-color threshold technique of Stiles and derived component color mechanisms. In: Jameson D, Hurvich L (eds): Visual Psychophysics, Handbook of Sensory Physiology. Vol II/4. Berlin: Springer-Verlag, 1972

42. Rushton WAH. The Ferrier lecture. Visual adaptation. Proc R Soc Lond B 162:20, 1965

43. Rushton WAH: The sensitivity of rods under illumination. J Physiol 178:141, 1965

44. Crawford BH: The effect of field size and pattern with the change of visual sensitivity with time. Proc R Soc Lond B 123:94, 1940

45. Blakemore C, Rushton WAH: Dark adaptation and increment thresholds in a rod monochromat. J Physiol (Lond) 181:612, 1965

46. Krill AE, Martin D: Photopic abnormalities in congenital stationary night-blindness. Invest Ophthalmol Vis Sci 10: 625, 1971

47. Heckenlively JR, Weleber RG: X-linked recessive cone dystrophy with tapetal-like sheen. Arch Ophthalmol 104: 1328, 1986

48. Carr RE, Gouras P: Oguchi's disease. Arch Ophthalmol 73:646, 1965

49. Dryja TP, Berson EL, Rao VR et al: Heterozygous missense mutation in the rhodopsin gene as a cause of congenital stationary night blindness. Nat Genet 4:280, 1993

50. Dryja TP, Hahn LB, Reboul T et al: Missense mutation in the gene encoding the alpha subunit of rod transducin in the Nougaret form of congenital stationary night blindness. Nat Genet 13:358, 1996

51. Sandberg G, Pawlyk BS, Jeffery D et al: Rod and cone function in the Nougaret form of stationary nightblindness. Arch Ophthalmol 116:867, 1998

52. Cideciyan AV, Zha XY, Nielsen L et al: Null mutation in the rhodopsin kinase gene slows recovery kinetics of rod and cone phototransduction. Proc Natl Acad Sci USA 95:328, 1998

53. Yamamoto S, Khani SC, Berson EL et al: Evaluation of the rhodopsin kinase gene in patients with retinitis pigmentosa. Exp Eye Res 65:249, 1997

54. Khani SC, Nielsen L, Vogt TM: Biochemical evidence for pathogenicity of rhodopsin kinase mutations correlated with the Oguchi form of congenital stationary night blindness. Proc Natl Acad Sci USA 17:2824, 1998

55. Yamamoto H, Simon A, Eriksson U et al: Mutations in the gene encoding 11-cis retinol dehydrogenase cause delayed dark adaptation in fundus albipunctatus. Nat Genet 22:188, 1999

56. Jay M: On the heredity of retinitis pigmentosa. Br J Ophthalmol 66:405, 1982

57. Molday RS: The Friedenwald lecture. Photoreceptor membrane proteins, phototransduction, and retinal diseases. Invest Ophthalmol Vis Sci 39:2493, 2000

58. Dryja TP: Molecular genetics of retinitis pigmentosa. Hum Molec Genet 4:1739, 1995

59. Krill AE: Hereditary retinal and choroidal diseases. New York: Harper & Row, 1972.

60. Carr RE: Vitamin A deficiency. In Heckenlively JR, Arden GB (ed): Principles and Practice of Clinical Electrophysiology of Vision, pp 737–740. St Louis: Mosby, 1991.

61. Hussaini SH, Henderson T, Morrell AJ et al: Dark adaptation in early primary biliary cirrhosis. Eye 12:419, 1998

62. Rayner RJ, Tyrrell JC, Hiller EJ et al: Night blindness and conjunctival xerosis caused by vitamin A deficiency in patients with cystic fibrosis. Arch Dis Childhood 64:1151, 1989

63. Cideciyan AV, Pugh EN, Lamb T et al: Rod plateaux during dark adaptation in Sorby's fundus dystrophy and vitamin A deficiency. Invest Ophthalmol Vis Sci 38:1786, 1997

64. Ernest JT, Krill AE: The effect of hypoxia in visual function. Invest Ophthalmol Vis Sci 10:323, 1971

65. Havelius U, Bergquist D, Falke P et al: I. Impaired dark adaptation in symptomatic carotid artery disease. Neurology 49:1353, 1997

66. Havelius U, Bergquist D, Hindfelt B et al: II. Improved dark adaptation after carotid endartectomy. Evidence of a long-term ischemic penumbra? Neurology 49:1360, 1997

67. Dannemiller JL: The early phase of dark adaptation in human infants. Vision Res 25:207, 1985

68. Hansen RM, Fulton AB: Electroretinographic assessment of background adaptation in 10-week-old infants. Vision Res 31:1501, 1991

69. McFarland RA, Fisher MB: Alterations in dark adaptation as a function of age. J Gerontol 10:424, 1956

70. Coile DC, Baker HD: Foveal dark adaptation, photopigment regeneration, and aging. Vis Neurosci 8:27, 1992

71. Jackson GR, Owsley CR, Cordle EP et al: Aging and scotopic sensitivity. Vision Res 38:3655, 1998

72. Pulos E: Changes in rod sensitivity through adulthood. Invest Ophthalmol Vis Sci 30:1738, 1989