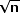| One of the most common questions asked by clinicians (and one of the
hardest to answer sensibly) is, “What does my sample size
need to be?” The answer to this grows out of the discussion above
on type I and type II errors. Obviously, the investigator would like
to design the study so that the risk of committing either type of error
is kept small. In the simple case of a clinical trial of two therapies, a
reasonable goal is to be able to reach one of two conclusions: Either (1) there is a statistically significant difference
between treatments, or (2) there is no clinically important
difference between the two treatments. Of course, in the first case, one
would also want to report the direction and magnitude of the difference. Unfortunately, some experiments that fail to show a statistically significant
difference also fail to rule out the possibility of a clinically
important difference. This result is not very satisfying to the investigator, the
statistician, or the reader, but it is a definite possibility
when the sample size is too small. Sample size calculations are
designed to help the investigator choose a sample size that will provide
a reasonable chance that the results will be statistically significant
at some specified level if there is a clinically important difference
between the two treatments. To compute a sample size (or use one of the many available tables), the
investigator must answer three questions: - What probability level should be defined as “significant?”
- What constitutes a “clinically important difference?”
- What should be used as the probability of a type II error?
These issues are discussed in the next section. WHAT PROBABILITY LEVEL SHOULD BE DEFINED AS “SIGNIFICANT?” The conventional 0.05 level may be chosen, or if multiple tests are going
to be made on the data, it may be more appropriate to use a more stringent
criterion, such as 0.01. This probability is called the α-level. When
the null hypothesis is true, α represents the
probability the experimenter will commit a type I error. WHAT CONSTITUTES A “CLINICALLY IMPORTANT DIFFERENCE?” This decision is a difficult one and not to be taken lightly. An alternative
way of stating it if you are the investigator is to ask yourself
what is the smallest difference you would be willing to take a chance
on missing. The smaller the difference, the larger the sample size necessary
to detect it. Clinicians (and some statisticians) often make a mistake here
and specify the difference they hope exists, not realizing that this policy means that should the difference
between treatments be smaller than anticipated (but nonetheless
important), there is no assurance that it will be found to be “statistically
significant.” WHAT SHOULD BE USED AS THE PROBABILITY OF A TYPE II ERROR? How sure does the investigator want to be of picking up a clinically important
difference if one exists? Conversely, how large a chance is he
or she willing to run of missing a clinically important difference? The
chance of a type II error, or missing a specified difference, should
it exist, is called the β-value. The complement of β, the
chance of detecting the difference, is called the “power” of
the experiment. Only an infinite sample size will be 100% powerful. It
is common practice to design experiments with 90% power, or
a β-value of 0.10. This means that if the difference
between treatments is really as large as that specified as “clinically
important,” the experiment has a 90% chance
of yielding results that are statistically significant at the specified
level. At first, 10% may seem like a large risk to take of
missing the difference. In actual practice, the risk is not as great
as it would appear. Even if the results are not “statistically
significant” at the end of the experiment, any important differences
are likely to show up as strong trends that suggest that further
investigation is warranted. When the above-mentioned assumptions are in hand, standard formulas
and tables are available for computing the required sample size. The
exact formula to be used depends on the type of variable to be observed (e.g., Is “effectiveness” to be evaluated by comparing
percent successes or average values of a quantitative variable?) and
the statistical tests to be employed (Will we use a two-tailed
test? Will we adjust for lack of continuity?). As an example of how sample size calculations are done, consider a clinical
trial with two groups of patients to be randomly assigned to treatment
A and treatment B, and some immediate effect will be observed to
determine “success” or “failure.” Table 1 could be used to find the required sample size as follows: Suppose treatment
A is known to have a 50% failure rate. Suppose further that
this is a simple short-term experiment with a straightforward
one-time analysis so it is reasonable to use 0.05 as the cutoff
point for “significant.” Although the investigators have
great hopes that treatment B will reduce the failure rate to 10%, cutting
failures in half would be important clinical news. Therefore, the
experiment might be designed to have a high (90%) probability
of detecting a difference in failure rates at least
as large as 50% versus 25%. Furthermore, if it should turn
out that treatment B is actually worse, that would also be an important
finding, so a two-tailed test should be employed. Table 1 shows that the required sample size is 77 patients in each group for a
total of 154 for this set of assumptions (α = 0.05, β = 0.10, p1 = 0.5, p2 = 0.25). Formulas appropriate to other situations are available
in standard texts. Table 1. Sample Sizes: Number of Patients Needed in Each of Two Groups*
| | P1 |
| P2 | 0.05 | 0.10 | 0.15 | 0.20 | 0.25 | 0.30 | 0.35 | 0.40 | 0.45 | 0.50 |
| 0.05 | | 581 | 187 | 100 | 65 | 46 | 35 | 28 | 22 | 19 |
| 0.10 | 581 | | 916 | 266 | 133 | 82 | 56 | 42 | 32 | 25 |
| 0.15 | 187 | 916 | | 1210 | 334 | 161 | 96 | 65 | 47 | 35 |
| 0.20 | 100 | 266 | 1210 | | 1462 | 392 | 184 | 108 | 72 | 51 |
| 0.25 | 65 | 133 | 334 | 1462 | | 1672 | 439 | 203 | 117 | 77 |
| 0.30 | 46 | 82 | 161 | 392 | 1672 | | 1840 | 476 | 217 | 124 |
| 0.35 | 35 | 56 | 96 | 184 | 439 | 1840 | | 1966 | 502 | 226 |
| 0.40 | 28 | 42 | 65 | 108 | 203 | 476 | 1966 | | 2050 | 518 |
| 0.45 | 22 | 32 | 47 | 72 | 117 | 217 | 502 | 2050 | | 2092 |
| 0.50 | 19 | 25 | 35 | 51 | 77 | 124 | 226 | 518 | 2092 | |
* p1, p2 = binomial proportion groups 1, 2; alpha = 0.05, beta = 0.10
DESCRIBING DATA FROM FOLLOW-UP STUDIES A common problem encountered in ophthalmology is describing the results
of a long-term follow-up study in which patients enter
at various points in time and are watched for months or years for the
occurrence of some event such as retinal detachment or loss of vision. Too
often, the results of this type of study are summarized with a statement
such as the following: “110 patients with disease x were
observed for periods ranging from 1 to 3 years (mean follow-up, 24.0 months). Twenty-five of the 110 patients (22.7%) became
blind during the follow-up period.” Unfortunately, statements like those in the last section are not as informative
as they sound and do not use the available data to the fullest. Indeed, the
type of summary illustrated above may even be misleading, especially
if interpolations (such as approximating the blindness
incidence rate as 11% per year) and comparisons are made
using the results as stated. A much better method for summarizing follow-up data is the technique
commonly called survival or life-table analysis. In this type
of analysis, an “event” such as blindness or death is
defined and all patients are followed until the event occurs or until
the date of analysis. The length of follow-up is then computed
for each patient as the time elapsed from entry into the study to the
event or date of analysis, whichever comes first. The cumulative proportion
with an event is calculated for each point in follow-up time, as
shown in Figure 4 from the Diabetic Retinopathy Study. 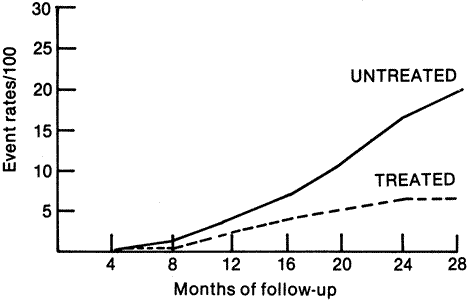 Fig. 4. Cumulative event rates of visual acuity less than 5/200 at two or more
visits for all patients. (Redrawn from Diabetic Retinopathy Study
Research Group: Preliminary report on effects of photocoagulation therapy. Published
with permission from The American Journal of Ophthalmology 81:383–396, 1976. Copyright © The Ophthalmic Publishing
Company.) Fig. 4. Cumulative event rates of visual acuity less than 5/200 at two or more
visits for all patients. (Redrawn from Diabetic Retinopathy Study
Research Group: Preliminary report on effects of photocoagulation therapy. Published
with permission from The American Journal of Ophthalmology 81:383–396, 1976. Copyright © The Ophthalmic Publishing
Company.)
|
One easy method of computing the cumulative probability of an event is
illustrated in Table 2, which contains real data on the occurrence of severe visual loss in untreated
senile macular degeneration. The first step is to compute some
probabilities of not having an event. (In life-table terminology, not having an
event is called “survival,” an unfortunate choice from the
ophthalmological viewpoint.) First, an interval survival is computed
for each point in follow-up time as the number of patients (eyes) “surviving” that time point (passing
through without an event) divided by the number at risk (those
followed up to the interval without an event). It is easy to
show that the cumulative survival at any time is the product of all
preceding interval survivals. The cumulative survival for time zero (start
of the study) is not shown on the table but always equals
one. Table 2. Life-Table Computations: Development of Severe Visual Loss in
Eyes With Parafoveal Neovascular Membranes Due to Senile Macular Degeneration
Interval
(i) | Number of Eyes in “No Treatment” Group |
B
At Risk | C
With Event | D
Interval Survival
1 – C/B | E
Cumulative Survival
D (E1–1) | F
Cumulative Event Rate
1 – E |
| 6 | 84 | 24 | 0.71 | 0.71 | 0.29 |
| 12 | 39 | 11 | 0.72 | 0.51 | 0.49 |
| 18 | 13 | 3 | 0.77 | 0.39 | 0.61 |
(Adapted from Macular Photocoagulation Study Group: Argon laser photocoagulation
for senile macular degeneration. Arch Ophthalmol 100:912–918, 1982. Copyright © 1982, American Medical Association)
Life tables have the advantage of using the full information on patients
followed for various lengths of time. Patients who entered the study
too late to be observed for the full time of the analysis are called “withdrawals” in life-table terminology because they
are withdrawn from the computations for certain time intervals. Clearly, they
are not withdrawn from the study, however, and are considered
at risk for as long as they were observed. True dropouts (i.e., patients
who refuse to or are unable to return) are analyzed the
same way as withdrawals, but the investigator needs to remember that
one important requirement of life tables is that all withdrawals be subject
to the same probability of an event as nonwithdrawals. No method (including
life tables) can adjust for the bias inherent in
failure to obtain complete follow-up. Life tables are usually presented in the form of a graph. Either the cumulative
proportion with an “event” or the proportion “surviving” without an event may be illustrated. | 

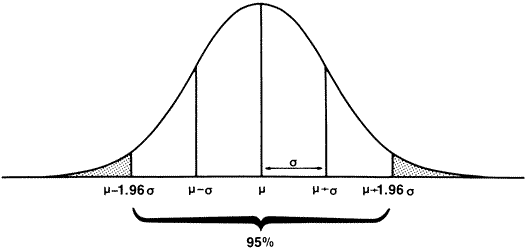
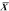 , the
sample mean or average, is an estimate of the true mean, μ, for
the population and SD or s is used to denote an estimate of σ, the
population standard deviation. A common way to represent results
is to give the “mean ± 1 SD.” For example, the data
in
, the
sample mean or average, is an estimate of the true mean, μ, for
the population and SD or s is used to denote an estimate of σ, the
population standard deviation. A common way to represent results
is to give the “mean ± 1 SD.” For example, the data
in 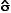 )
)