
|
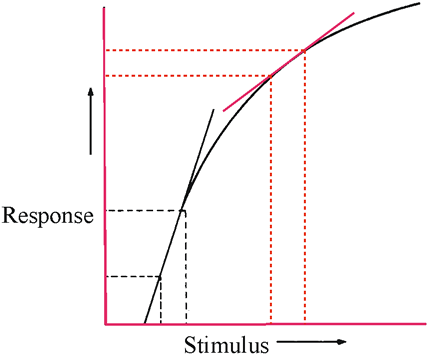
| Fig. 26. Linearity and the first-order kernel of a nonlinear system. A strong reliable first-order kernel does not mean that the system or the response is linear. Linear estimates of a nonlinear process are highly dependent on the stimulus values used, such as mean luminance or contrast. Consequently, different experiments can yield very different estimates of the first-order kernel. The solid line represents a logarithmic nonlinearity such as might be imagined for the retina. The dotted lines indicate the limits of the stimulus conditions (abscissa) and the observed responses (ordinate). The straight lines or “linear estimates” fitted through the two regions are very different, reflecting the underlying nonlinearity of the function they are estimating. Similarly, the underlying nonlinearity of the visual system implies that first-order kernels obtained under different conditions will differ because of the nonlinear behavior they estimate. This limitation does not deny clinical utility of the technique. (Adapted from Odom.136) |