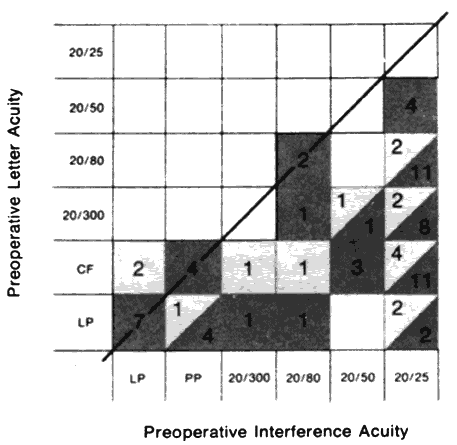
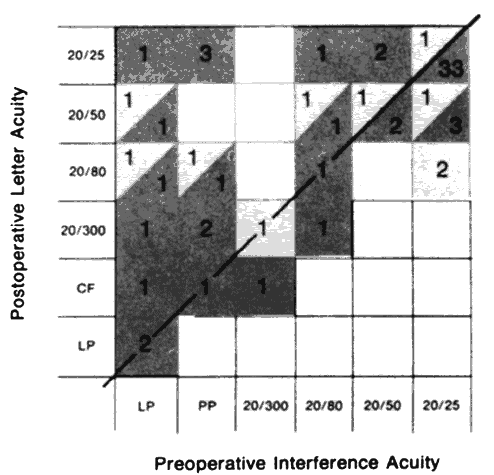
The principle of generating low-frequency patterns by having two periodic waves go in-phase and out-of-phase with one another is precisely the means used to produce interference fringes with a laser light source. In this instance, however, the waves occupy different positions in space rather than differing in frequency (Fig 2). Divergent spherical wavefronts are produced by two separate point sources of light. The wavefronts move through space with a velocity c. The circular lines represent the crests of the waves. The separation between two adjacent crests is; λ, the wavelength. It may be helpful to think of the crests as ripples produced on the surface of water. For example, imagine a stone repeatedly dropped into water and a cork floating on water some distance away. The ripples cause the cork to bob. When two stones are simultaneously dropped into the water, each setting up wave motion, what happens depends on the relative phases of the two sets of waves at each point in space. At the intersection lines in Figure 2 the crests overlap. At these points the wave motions from the two sources are in-phase and the effect of superposition is to produce resultant motion of larger amplitude. Bright bands in the interference fringe pattern are produced through the addition of in-phase waves. As one moves along the screen, the relative distance from the two sources changes so that at other points the crests of one wave occupy exactly the same positions as the troughs of the other alone. The result of superposition is then complete extinction of wave motion, causing dark bands (Fig 3). The angle between fringes varies inversely with the separation between the interfering sources. The inverse relationship is not difficult to understand, if one considers the two extreme cases where the sources are either very far apart or very close together. If the sources are far apart, the interfering wavefronts will arrive at the midpoint on the screen from nearly opposite directions. If the waves are in phase, one only has to move a distance of λ/2 they will be out-of-phase.* In other words, the fringe frequency will be exceedingly high. On the other hand, if the two sources are nearly coincident, the waves will be in-phase over great distances on the screen and the fringe frequency will be very low.
|
|
* A wave traveling in the positive x direction can be written
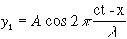
Likewise a wave in the negative x direction is given by
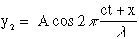
The sum is
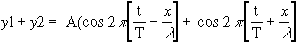
Introducing the expression for the cosine of the sum and difference of two angles,
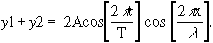
A cosine curve results in which amplitude varies in time. The distance between adjacent points where the fluctuations are maximum is λ/2
ADVANTAGES
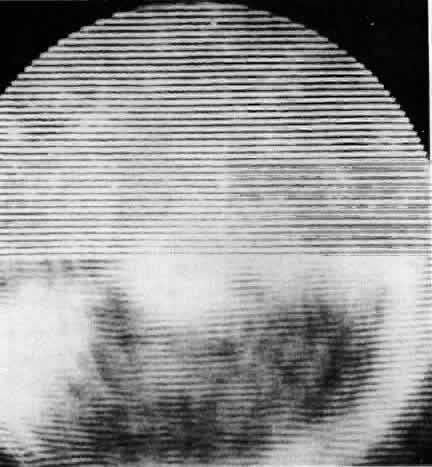
To understand how it is possible to produce fringes directly in a patient's eye, one should substitute the retina for the screen and imagine two sources of monochromatic light imaged directly into the eye so that the dark and light fringes are formed on the retinal surface. These fringes are different from the images formed by the patient's simply viewing a pattern of colored stripes, because when the patient views a striped target, optical aberrations spread light from the bright areas into the dark areas, leading to a loss of contrast in the retinal image. With interference fringes, however, this does not happen. When the waves from the sources are out-of-phase, they cancel, forming a dark area; when they are in-phase, they add, producing a bright area. Consequently, the interference fringes formed by two sources of equal intensity are always of very high contrast, independent of aberrations. It is for this reason that fringes are said to bypass the effects of the eye's dioptrics.
Light scattering might be expected to adversely affect fringes and ordinary images equally, but observation shows this is not the case. If sufficient layers of tissue paper or Mylar drafting sheets are stacked to reduce visual acuity to light perception, interference fringes can still be clearly seen by the normal eye when light is projected through the layers.
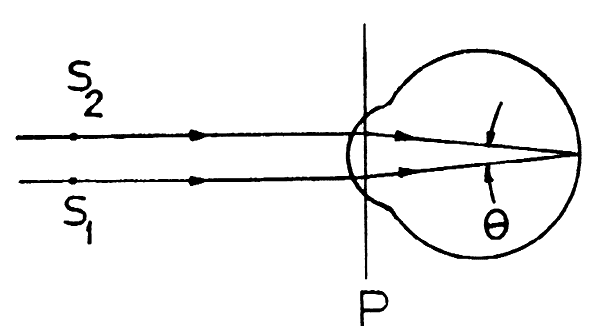
Let us consider now the dependency of the retinal pattern on the position of the double sources. In Figure 4, the image-forming properties of the eye are represented by the reduced schematic eye. Two rays parallel to the optic axis are shown. They will be refracted and come to a point focus on the retina. Imagine the sources to be at some arbitrary distance from the observer, with one source on the uppermost ray and the other on the lowermost ray. The rays from the sources parallel to the optic axis are refracted to form angle 0, independent of distance.† It is this angle which determines the fineness of the fringe pattern. Thus, for the creme-tropic eye, the fringe frequency is completely independent of the distance from the eye to the double sources. Even if the eye is not emmetropic, when the double sources are imaged near the nodal points, the relationship between the separation of the double images and the fineness of the grating pattern is given by equation 1.
|
†If two beams of monochromatic light from a coherent source are focused in the plane of the pupil, α, the angular separation of successive maxima in the intensity distribution on the retina can be expressed as follows:
α = λ/a
(1)
where α is in radians, λ is the wavelength of the light in air, and a is the separation between the double sources in air.
Equation 1 is actually an expression for the angular distance between bright fringes, with respect to the point midway between the line connecting the two sources. This angular distance depends only on wavelength and separation between the sources. The distance between fringes on the screen of Figure 2, of course, depends also on the distance, D, from the sources to the screen. If we let x be the distance between maxima in the intensity distribution on the screen, since x is much smaller than D, the angular distance and the linear distance are related by α =x/D
Equation 1 can then be rewritten as
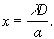
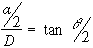
For the very small angles the tangent can be approximated by the angle in radians so the following equation is obtained:
= a/D