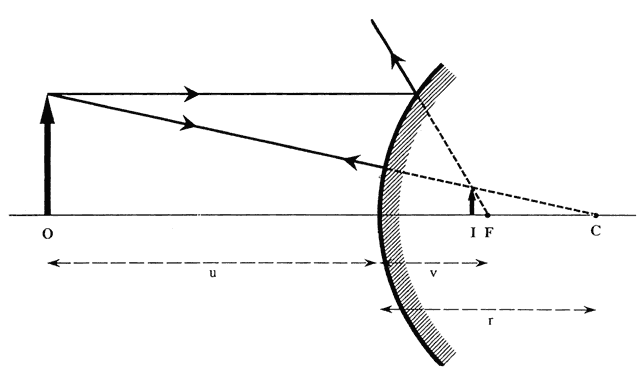
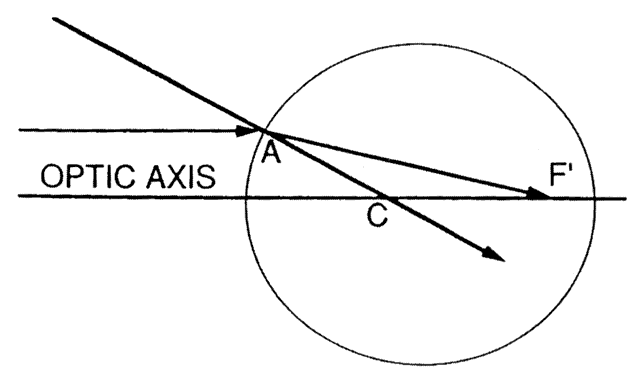
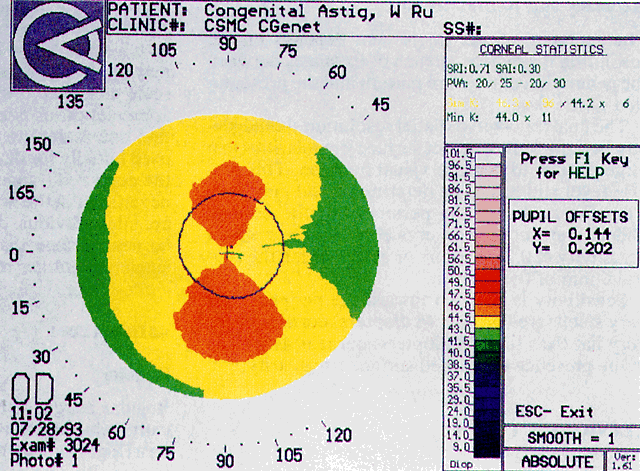
The first known keratoscope target was the image of a window, as reported by Scheiner in 1619 using natural light. He estimated the corneal curvature by comparing the window pane corneal reflection to those of a series of marbles until he found one that gave an image the same size as that of the cornea.1 In 1820 Cuignet developed a keratoscope through which he observed the reflected image of an illuminated target held in front of a patient's cornea. His major problem was in the alignment of the light, target, and observer with the patient's visual axis. This was overcome in 1882 by Placido, who placed an observation hole in the center of the target.2 Placido's target of alternating black and white rings (the Placido disk) has been embodied in many devices that are currently used to measure corneal topography, hence the term Placido disk keratoscopy.
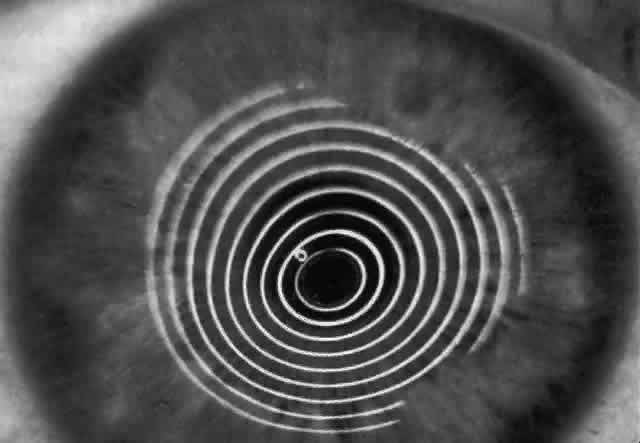
A modern version of the original Placido disk is the Klein hand-held keratoscope (Fig. 1). This device is useful for detecting the location of tight sutures, irregular astigmatism, and keratoconus, all of which can be detected by mire pattern recognition. Its main limitations are that its mire pattern has an outer diameter of 5.5 mm, limiting its utility for evaluating peripheral topography. In addition there is no mechanism to achieve alignment other than user estimation, which introduces significant error in subjective interpretation.1 Photokeratoscopes (e.g., Corneascope: Keravision, Santa Clara, CA) project a series of concentric circular mires that form a virtual image located within the anterior chamber of the eye. Information regarding the power of the anterior corneal surfaces is derived from visual inspection of the size and shape of the mires.
|
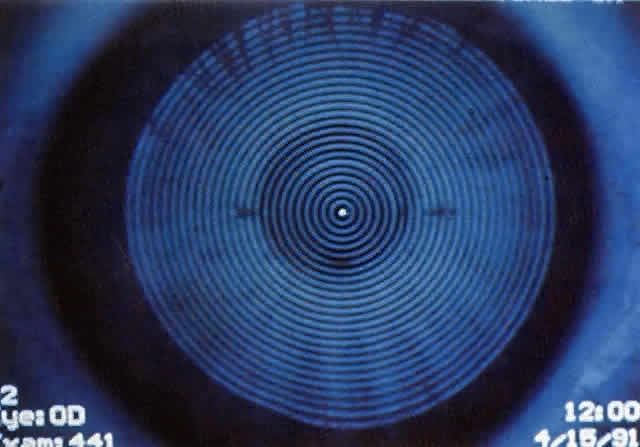
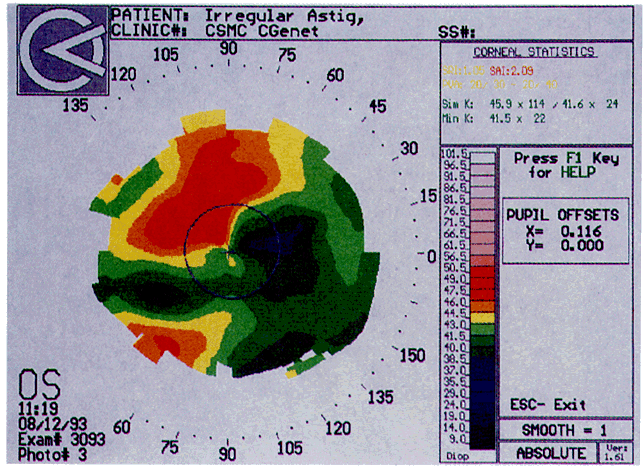
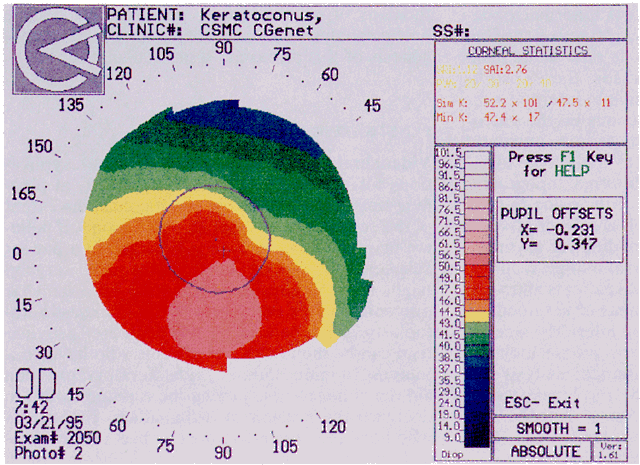
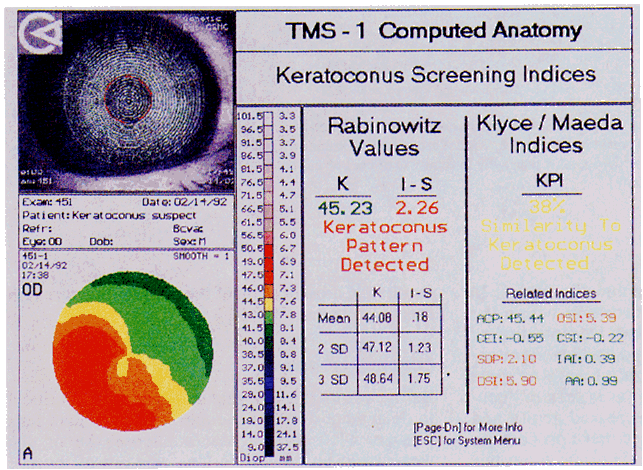
Simultaneously, information regarding the radius of curvature of a localized area of the cornea can be obtained by observing the separation between the mires reflected from that area of the cornea. In areas of steep cornea, the images of the mires are smaller, so the rings appear narrower and closer together. In the presence of regular astigmatism, the mires appear elliptic, the short axis of the ellipse corresponding to the meridian corneal steepening and highest power.3 Irregular astigmatism produces nonelliptic distortion of the mires. For the most part, photokeratoscopes yield qualitative information that is clinically useful as a means of evaluating changes in the peripheral cornea, such as in the detection of the corneal ectasia associated with keratoconus (Fig. 2), or as a guide to selective suture removal after penetrating keratoplasty. Its limitations are that it provides no information about the central 3 mm of the cornea and that up to 3 diopters of cylinder may go undetected by visual inspection of photokeratographs.
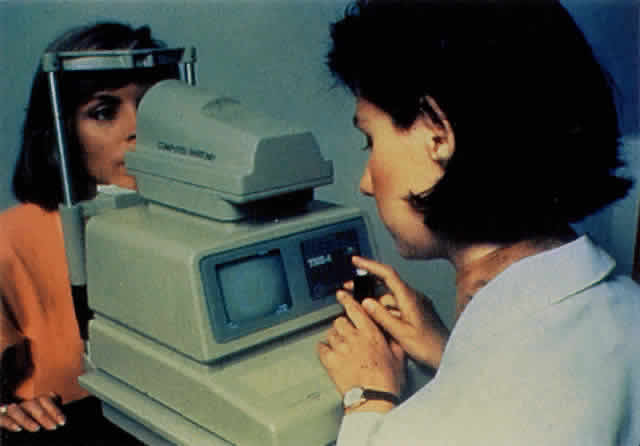
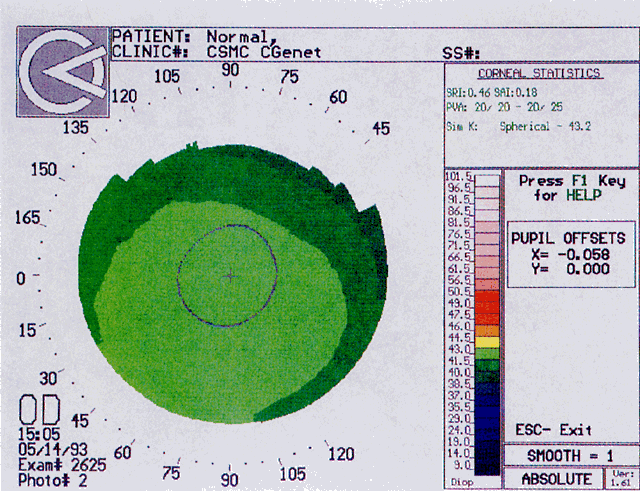
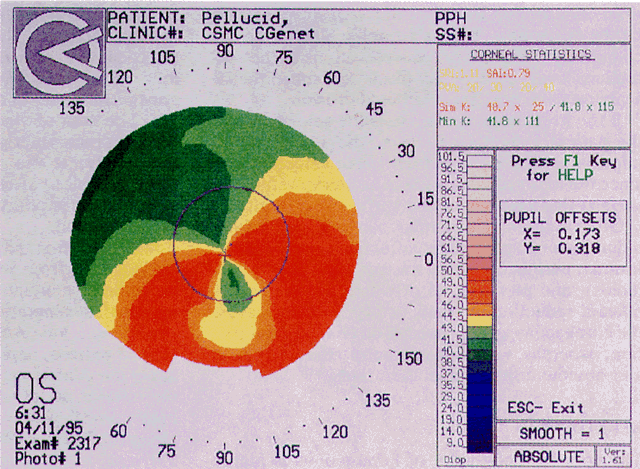
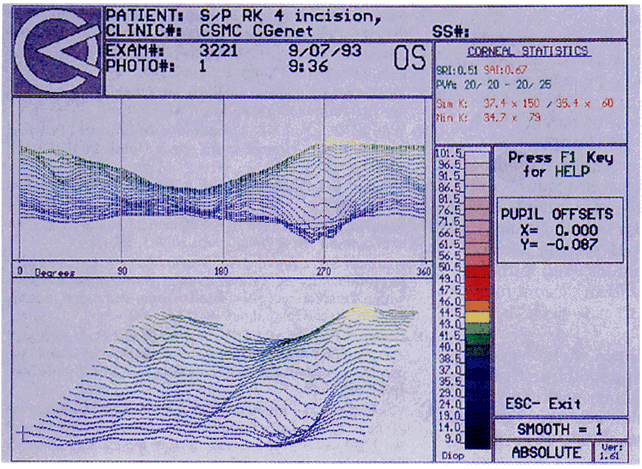
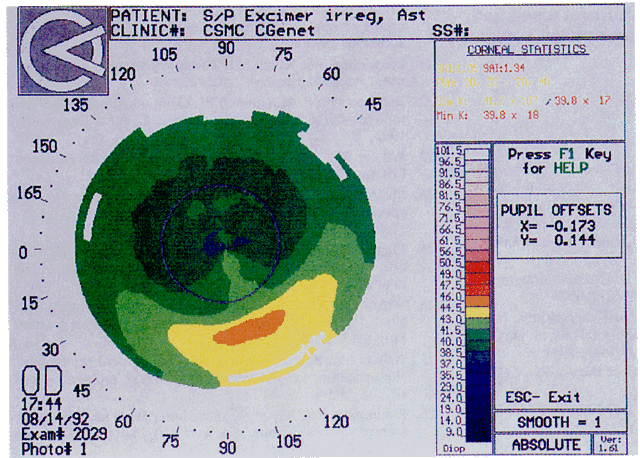
Quantitative analysis of photokeratograms became practical when Gullstrand in 1896 applied photography to keratoscopy (photokeratoscopy).3 This allowed the clinician to fix the image and measure the size of the rings; however, this analysis is slow and subject to major errors.3 In the 1980s, computer power was adapted to the task of automated high-resolution corneal topography analysis, which is most popularly implemented in commercially available computer-assisted videokeratoscopes, such as the Topographic Modeling System (TMS-1) (Computed Anatomy, New York, NY) and the Corneal Analysis System (Eysys Laboratories, Houston, TX). These devices were devised in order to overcome the deficiencies of photokeratoscopes both in speed and in gathering quantitative information about the anterior corneal surface.4 Most systems use illuminated Placido-type mires with nosecones that provide a broad area of corneal coverage from the apex to the limbus of the cornea, covering approximately 11 mm of cornea (Fig. 3). These novel conical mire targets provide very high radial resolution, being approximately 0.17 mm apart reflected on the normal corneal surface. Additionally, the central fixation light and the first mire of the standard cone provide excellent central corneal coverage, ensuring that corneal topographic details important to visual function are not obscured as they are with keratometers and traditional keratoscopic targets. Because direct measurements are made from the centrally visually important area as well as from the periphery, a clinically complete data set derived from between 6000 and 11,000 data points on the cornea is available for clinical interpretation. Other advantages of videokeratoscopy over photokeratoscopy are its speed in gathering quantitative information and its ability to display data in a clinically useful format with reasonable accuracy.5–7
|