CORNEA
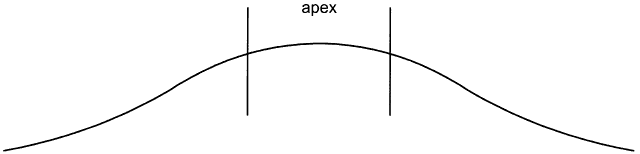
To fit contact lenses well, one must understand the contour of the cornea. The corneal surface is not a sphere; rather, it is aspheric, with an apical zone6–9 (Fig. 1). This zone is the area of the cornea over which the corneal curvature is regular or constant. Several topography devices have been invented to enable the practitioner to understand the contour of a particular patient's cornea.
|
KERATOMETRY
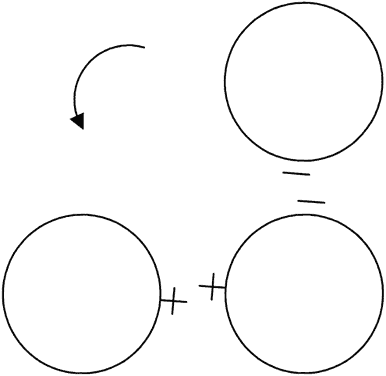
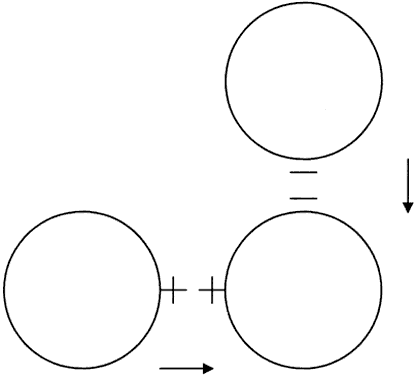
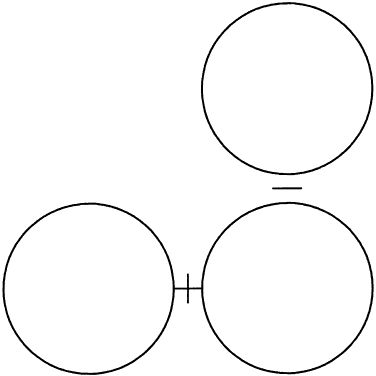
Although topography devices are available, rigid lenses still are fitted based on keratometry. We perform keratometry to measure the curvature of the apical zone. Never forget that the keratometer actually measures the distance between two points 3 mm apart on the cornea. The keratometer produces patterns that are reflected back from the cornea; these are viewed as mires. Mires first must be aligned by rotating the barrel of the keratometer (Fig. 2). Once the barrel of the keratometer is rotated, then the mires are partially aligned (Fig. 3). The next step is to rotate each drum (horizontal and vertical) until the “+ ” and “-” mires are superimposed (Fig. 4). After the mires are aligned, each of the two drums on the keratometer yields a meridional reading in both millimeters and diopters (D). In this chapter, diopters are used. An example of such a reading is 42.00 D @ 180° and 44.00 D @ 90°. The final keratometry readings (“K readings”) are written in a shorthand form as the flatter (smaller) reading in diopters, followed by the steeper (larger) reading in diopters, followed by the meridian of the steeper reading, for example, 42.00/44.00 @ 90°. The flatter meridian is called “K,” and rigid lens fitting always is based on this number. In this example, K is 42.00 D.
|
|
ASTIGMATISM
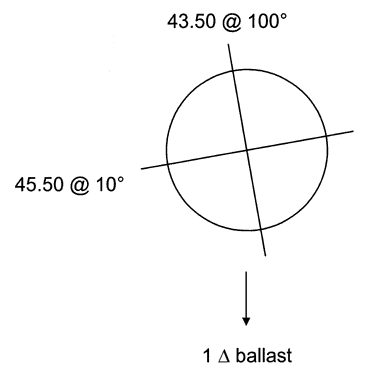
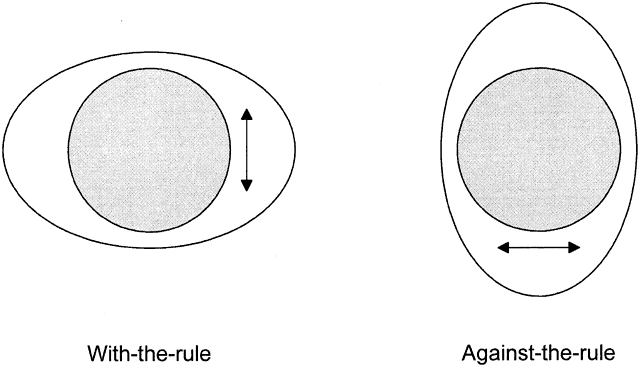
Keratometry can show whether corneal astigmatism is with the rule or against the rule. With-the-rule astigmatism means that the corneal “egg” is lying on its side; against-the-rule astigmatism means that the egg is standing on end (Fig. 5). Here are keratometric examples:
|
| With-the-rule: | 42.00/44.00 @ 90° |
| Against-the-rule: | 42.00/44.00 @ 180° |
Rigid contact lenses have a tendency to move along the steeper meridian. Thus, with-the-rule astigmatism is good for rigid contact lens fitting because the lens moves up and down with the blinking of the upper lid; against-the-rule astigmatism is not as good because the lens tends to move side to side with each blink. Usually, corneal astigmatism is with-the-rule, hence the name.
Thus far, we have considered only corneal astigmatism, which is measured with a keratometer. In clinical practice, we also measure refractive astigmatism. Whereas keratometry measures only corneal astigmatism, refraction measures a combination of both corneal and residual astigmatism. Residual astigmatism also is called lenticular astigmatism because it is believed to originate from a tilted crystalline lens. We decide which contact lens to fit based on how well the refractive astigmatism and the keratometric astigmatism match.
Following is an example of matching astigmatism, where the corneal shape is responsible for the entire refractive astigmatism; a simple rigid lens would work well because a rigid lens cancels out corneal astigmatism:
| Keratometry: | 42.00/44.00 @ 90° |
| Refraction: | -3.00 + 2.00 × 90° |
Following is an example of residual astigmatism. Note that there is only 0.50 D of corneal astigmatism but 1.50 D of refractive astigmatism. The difference between the two, 1.00 D, constitutes the residual astigmatism. This difference requires toric lens fitting because a spherical rigid lens cancels out only corneal astigmatism:
| Keratometry: | 42.00/42.50 @ 90° |
| Refraction: | -3.00 + 1.50 × 90° |
LENS TYPES AND PARAMETERS
Lenses either are soft or hard. Soft contact lenses (SCLs) are “all alike” because they are made from hydrogels, water-containing soft material. Rigid lenses currently are made from RGP materials; the “old” hard lenses were made of PMMA, a plastic that was not oxygen permeable.
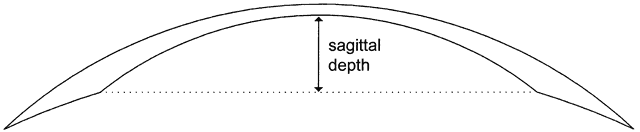
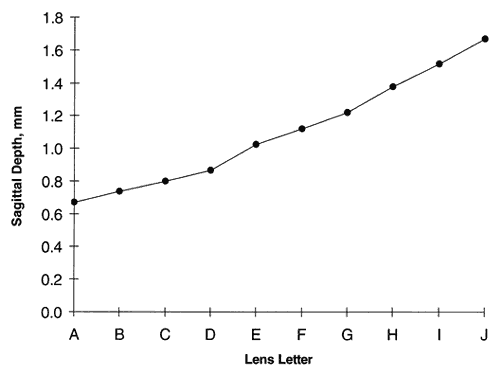
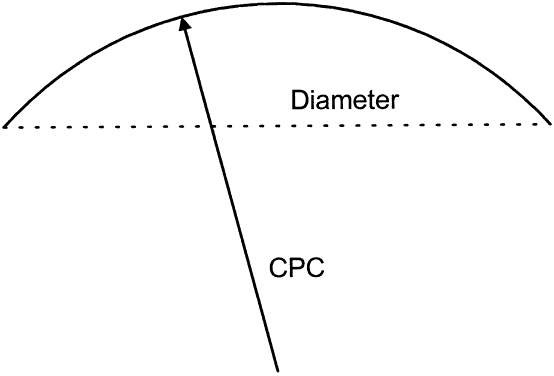
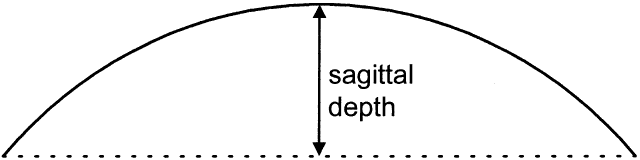
All contact lenses share the same important parameters: diameter, central posterior curve (CPC—also known as base curve, or BC), and power (Fig. 6). Diameter is measured in millimeters, CPC is measured in diopters (for rigid lenses) and millimeters (for SCLs), and power is measured in diopters. Diameter and CPC determine the sagittal depth of a lens (Fig. 7). No one has proven a numerical relationship between sagittal depth and lens fit, but most practitioners believe that an increase in sagittal depth for either a soft or rigid lens results in a more tightly fitting lens.10–13 Thus, the lens itself tightens as the sagittal depth increases. Increasing the diameter of a lens increases the sagittal depth to a great degree and also results in tight fitting.
|
|
TEAR LENS
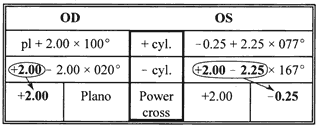
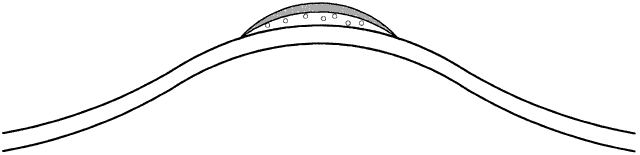
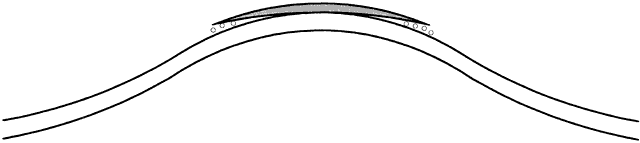
Lens power constitutes most, but not all, of the effective power of a rigid lens. Depending on its relationship to the cornea, the CPC also contributes to the effective power because it creates a “tear lens.” If a lens is “steeper than K,” it produces a tear lens that functions as a plus lens. This plus tear lens must be corrected in the final or prescribed lens power, by adding minus power (Fig. 8). Conversely, if the rigid lens is fitted “flatter than K,” then a minus tear lens is created, which needs to be corrected in the final or prescribed lens power by adding plus power (Fig. 9). The actual correction for the tear lens can be remembered as a mnemonic: SAM FAP—steeper, add minus; flatter, add plus.
|
|
MINUS CYLINDER THINKING
When we work with rigid lenses, we always convert to minus cylinder, then drop the cylinder. Why? We can answer this question in two steps:
- Because the cornea is a convex surface, any corneal astigmatism is a plus
cylinder. Such a refractive error is neutralized by an equal and opposite
power, that is, minus cylinder. Thus, we start by writing the refraction
in minus cylinder form.
- When we place a rigid contact lens onto the eye, the resulting concave
tear film is a minus cylinder, which automatically corrects the plus cylinder
of the astigmatic cornea. Thus, we can “drop the minus cylinder” and
consider only the resulting sphere power for the contact
lens.
Thus the rule, “Convert to minus cylinder and drop the cylinder.” An example of this idea is to take a refraction of -3.00 + 1.00 × 90°. We convert to minus cylinder form: -2.00 - 1.00 × 180°. By dropping the cylinder, we end up with a rigid contact lens power of -2.00 D. Remember that this calculation assumes that all refractive astigmatism is corneal in origin.
VERTEX DISTANCE CORRECTION
Any spectacle correction intended to be used for contact lens fitting needs to be corrected for vertex distance if the refraction is greater than + 4.00 or -4.00 D.
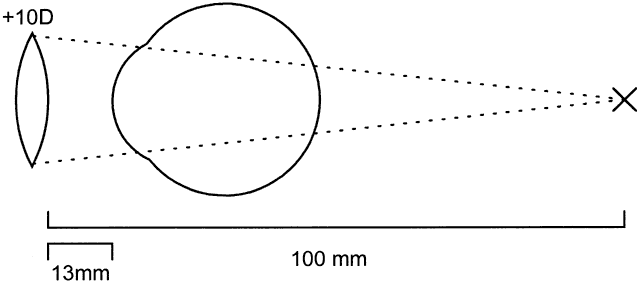
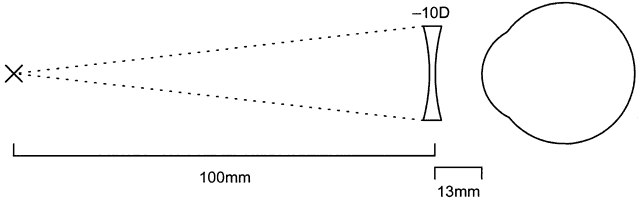
This concept is easier to understand with a couple of examples. We shall consider first a + 10 D and then a -10 D lens, both located 13 mm (vertex distance) from the eye.
In the first example, the focal length of a + 10 lens is (1000 mm/10) = 100 mm (Fig. 10). By placing a contact lens onto the eye, the focal length becomes shorter: 100 - 13 = 87 mm. Thus, the power of the contact lens is (1000/87) = + 11.50 D (rounded to nearest eighth of a diopter).
|
In the second example, the -10 lens has the same focal length (100 mm), but in the opposite direction (Fig. 11). When it is placed onto the eye as a contact lens, the focal length increases: 100 + 13 = 113 mm. Thus, the contact lens has a power of (1000/113) -8.87 D (rounded to nearest eighth of a diopter).
|
In both cases, for either plus or minus lenses, always add plus power when correcting for vertex distance.
LENS FITTING EXAMPLE
This is the type of problem seen on written examinations. We want to fit a rigid lens on a patient with the following readings:
| Keratometry: | 42.00/43.50 @ 90° |
| Refraction: | -9.00 + 1.50 × 90° |
Suppose the refraction was done with a vertex distance of 13 mm and that we want to fit 0.50 D steeper than K. What is the power of the final lens?
This type of problem is solved in three steps:
- Convert to minus cylinder. First we convert the refraction to minus cylinder
and drop the cylinder: -9.00 + 1.50 × 90° becomes -7.50 - 1.50 × 180°. Dropping the cylinder leaves -7.50.
- Correct for vertex distance. The focal distance of a -7.50 D lens is (1000/7.5) = 133 mm. In
converting for 13 mm vertex distance, the focal
length for the contact lens is (133 + 13) = 146 mm. The power of
such a lens is (1000/146) = -6.85 D. Note that we do not round off the
results at this point.
- Correct for lens fit. Because the lens is fitted 0.50 D steeper than K, we
add minus power (remember: SAM of SAM FAP): -6.85 - 0.50 = -7.35. Rounding
to the nearest eighth of a diopter yields the final answer: -7.37 D.
The K readings were not necessary to solve this problem. They often are included on examinations as red herrings. Also, I do not advise the actual fitting of lenses using this theoretical method of calculating the final lens directly from the refraction and keratometry. Nothing beats the actual placement of diagnostic contact lenses onto the patient's eyes. The following fitting methods use this philosophy.


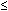 2 D).
2 D).