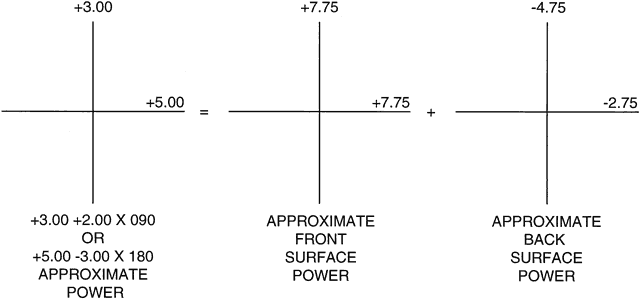
| A finished or edged spectacle lens that goes into a patient's frame
is made from a lens blank. Optical laboratories buy blanks from lens
manufacturers and then perform other operations such as surfacing (grinding
the proper power onto a surface of a lens), edging (cutting the
lens to the proper shape), tinting, and treating for impact resistance. The
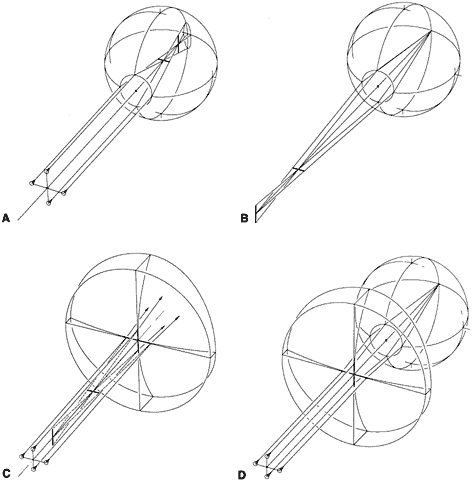
following three types of lens blanks are in use. ROUGH BLANK Glass lenses are formed by grinding and polishing a molded pressing or
rough blank (Fig. 14A). A pressing is a rough, unpolished piece of glass having a meniscus shape, with
the surface curves approximating those to be eventually ground
on it. Its diameter is that intended for the finished lens. Pressings
are usually formed immediately after a gob of molten glass is drawn
from the tank where the raw ingredients have been combined. Each gob
is pressed between the curved surfaces of a metal mold and allowed to
cool. Alternatively, the glass can be drawn from the tank and rolled
out into sheets that are cut into lens-sized squares, then shipped. In
the molding room of a lens manufacturer, these squares can be reheated
and formed into round meniscus-shaped pressings. Optical laboratories
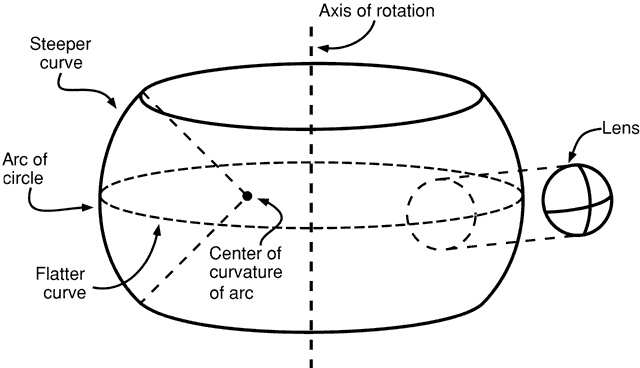
rarely use pressings. 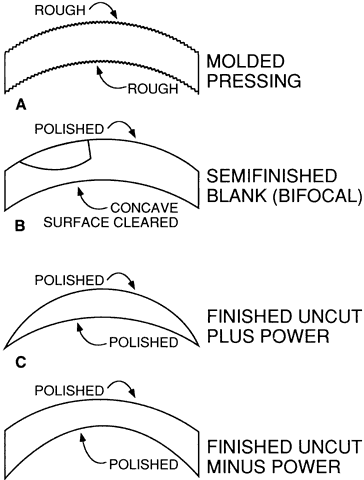 Fig. 14. Lenses are supplied as (A) molded blanks or pressings, (B) semifinished blanks, and (C and D) finished uncut lenses. Fig. 14. Lenses are supplied as (A) molded blanks or pressings, (B) semifinished blanks, and (C and D) finished uncut lenses.
|
SEMIFINISHED BLANKS A semifinished blank is a lens blank that has been finished on one surface (see Fig. 14B). Glass semifinished blanks are made from a pressing. The pressing is “blocked” or
attached to a holding device so that the front
surface can be ground and polished to the final power. If the lens is
to be a multifocal, a segment or segments must be constructed on the
lens front surface. The concave back surface is then given a short grinding
and polishing to “clear” the surface. This practice
improves the appearance, which is a competitive factor, and also facilitates
inspection of the surface and the interior of the glass itself. After
inspection, semifinished blanks are packaged and shipped from
the lens manufacturer to local optical laboratories through a variety
of distribution channels. The need for a fixed orientation of the multifocal segment prevents rotation
of a multifocal lens blank to obtain the proper cylinder axis. Therefore, multifocal
lenses are almost universally supplied as semifinished
blanks, and the back surface is surfaced by the optical laboratory
to obtain the proper lens power and to position the optical center
correctly relative to the multifocal segment. Some finished bifocal spheres
are available. Single-vision semifinished blanks usually are used
only for stronger-than-average lens powers that are not routinely available
as uncut lenses. Plastic semifinished blanks, which are usually multifocal lenses, are made
by pouring (CR-39, PPG Industries, Pittsburgh, PA) or injecting (polycarbonate) the
plastic into glass or metal molds, then cooling it at
a controlled rate. Polycarbonate blanks are then coated for abrasion
resistance. Any one semifinished blank may be used for a variety of prescriptions, depending
on what ocular (back) surface power is ground at the local laboratory. A
wide range of choices are possible, depending on the thickness
of the blank: the thicker the blank, the greater the latitude in
curve selection. Prescription accuracy at the optical center and the
control of off-axis lens aberrations restrict the choice. One of the objectives
of lens design is to design a “set” of these semifinished
blanks. This set or series of 10 to 20 lens blanks of different
front surface powers and center thicknesses, used in conjunction with
a chart of instructions, can provide for hundreds of well-designed
but different prescription items. An index of the quality of a series
of blanks is their number. Available series number from 4 to approximately 20. FINISHED UNCUT LENSES Finished lenses or finished “uncut” lenses have had both surfaces
ground to the final optical quality (see Figs. 14C and D). The steps are the same as those described previously, except that thinner
pressings or molds can be used because the lens power will not be
further modified. The savings in lens material and the lower labor costs
of mass production make this a less expensive route than semifinished
blanks for popular single-vision prescription items. However, even
in this procedure there are economic reasons for using a limited number
of surface powers and molds. The uncut single-vision lenses provided
by a lens manufacturer should be similar to those made by an optical
laboratory from semifinished blanks of the same manufacturer. This provides
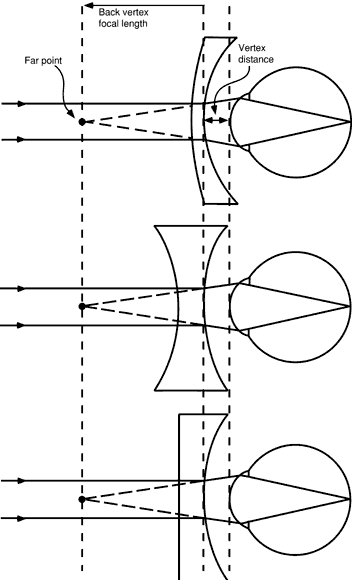
consistent patient response. The finished uncut lens must be edged or shaped to fit into a patient's
frame. “Layout” for edging includes rotation of the
lens to orient the cylinder axis properly and decentration of the lens
optical center to position it properly for the patient's interpupillary
distance (PD). Glass lenses are further processed after edging
to increase impact resistance, whereas plastic lenses may be tinted or
coated for abrasion resistance or to reduce reflections. The lenses
are then inserted into the frame, and the accuracy of the prescription
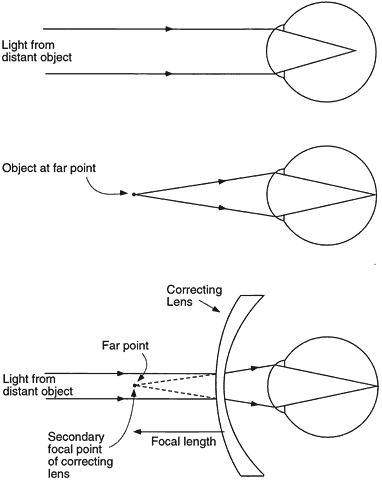
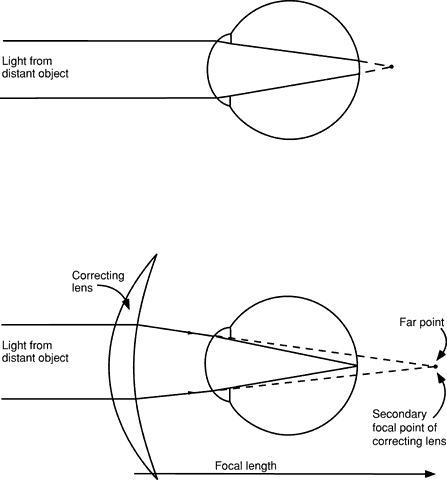
is verified. |  of a degree, so we call them parallel. In a refracting room, the rays
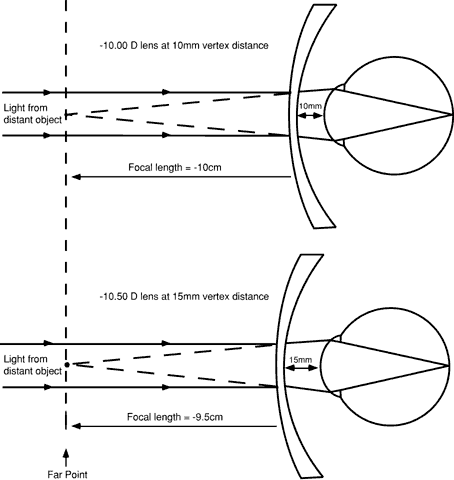
from a single point on a letter on the visual acuity chart are not quite
parallel. At 20 feet (6 m), the light rays have a divergent power of -0.16 diopters (D) as
they enter the refractor. At 10 feet (3 m), the
light rays diverge -0.33 D. Some doctors adjust for this factor when
they determine the spectacle prescription.
of a degree, so we call them parallel. In a refracting room, the rays
from a single point on a letter on the visual acuity chart are not quite
parallel. At 20 feet (6 m), the light rays have a divergent power of -0.16 diopters (D) as
they enter the refractor. At 10 feet (3 m), the
light rays diverge -0.33 D. Some doctors adjust for this factor when
they determine the spectacle prescription.