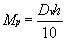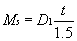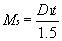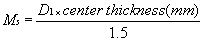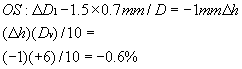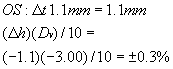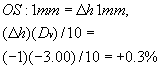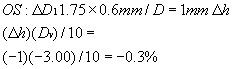BASIC CALCULATION The Thill Aniseikonia Worksheet is shown in Figure 1.  Fig. 1. Thill Aniseikonia Worksheet. Fig. 1. Thill Aniseikonia Worksheet.
|
Part I Each meridian must be compared with its opposite in the other eye, so it
is helpful to begin by putting the powers on an optical cross. (Most
axes are close to the vertical or horizontal.) Line 1: Using the patient's prescription, indicate the meridian closest to 180 and
to 90 degrees.
Line 2: Fill in the power in that meridian.
Line 3: The meridian that needs the magnification. Calculate the difference between
the two 180-degree meridians and put this difference in the column
that has the most minus or the least plus in the prescription. Do the same for the 90-degree meridian. If the axes
are at 45 and 135 degrees, use those meridians instead.
Line 4: Gross magnification required. The figure from line 3 is multiplied by 1% per
diopter. If some test was used for aniseikonia and a percentage
was found, skip lines 1, 2, and 3; use the test figure on line 4.
Line 5: Subtract 1%, which it is assumed the patient can tolerate.
Line 6: Gives the amount of magnification we will attempt to create.
Part II Using a surfacing chart and using minus cylinders to get a starting point, find
the front curve D1 and the center thickness with which the lens would ordinarily be fabricated. Calculate
the magnification from shape using this information, and
enter it into the space to the left: (eq 4) 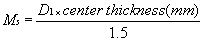
Part III Line 1: Use the figure with the higher front curve and center thickness for both
lenses. Enter this information in pencil (so that it can be modified
if necessary) in the correct lines to the right. Calculate Ms using the formula in equation 4.
Line 2: Experiment with how these figures should be changed to obtain the desired
magnification or minification required from line 6. Begin by decreasing
the curve on the lens that requires the minification. Calculate
Ms using this new, flatter curve.
Line 3: When magnification is close to that desired, a correction must be made
for the change in magnification due to the power factor, Mp, caused by this change in the front curve, D1. To do this we must know the change in the vertex distance created by
the change in D1. There is a relationship between curve and width of the lens, called sag:d 0.5 mm per diopter for a 44-mm lens
0.6 mm per diopter for a 48-mm lens
0.7 mm per diopter for a 52-mm lens
This means, for example, that for a 44-mm lens, if the front curve has
been changed by 1 D, the vertex distance changes by 0.5 mm.dFor a plus
lens:
| if (D1) is Thickness is | Vertex distance is | Resulting in |
| Increased | Increased | More Magnification |
| Decreased | Decreased | Less Magnification | Add this correction to the Ms found in line 2. If this does not give the required minification, decrease
center thickness slightly and recalculate Ms. Line 4: Correction in Mp (power factor) for the change in center thickness. Again, owing to change
in vertex distance, now due to the change in center thickness, another
correction in Mp is to be made. For plus lenses:
| If Center Thickness is | Vertex distance is | Resulting in |
| Decreased | Increased | More Magnification |
| Increased | Decreased | Less Magnification | Add this correction to the Ms found in Part II. If the magnification is still not the desired amount, go to the other lens
to increase the front curve and increase the center thickness, correcting
both changes for Mp changes as was done in the above (Fig. 2).  Fig. 2. Example 1: a plus lens problem. Fig. 2. Example 1: a plus lens problem.
|
Part IV For explanation, see later discussion Example 2, Minus-Lens Problem. EXAMPLE 1: A PLUS LENS PROBLEM The right eye requires a + 4.00-D lens and the left eye a + 6.00-D
lens. Vertex distance, h, is 10 mm, and the lens will be 50 mm wide (see Fig. 2). Part I The + 4.00 D is put on the optical cross for both horizontal and vertical
meridians for the right eye, and the + 6.00 D is put on the
optical cross for both horizontal and vertical meridians for the left
eye. Line 1: Since lenses are spheres, all the meridians are the same.
Line 2: Power will be + 4.00 D for both meridians on the right eye and + 6.00 D
for both meridians on the left eye.
Line 3: Difference is 2.00 D for both horizontal and vertical meridians and is
placed in the columns that have the least plus, the right eye in this
case.
Line 4: Magnification estimation is 1% per diopter, yielding 1% × 2.00 D = 2%.
Line 5: Subtracting the 1% assumed tolerance.
Line 6: Gives the amount of magnification desired as 1% in both meridians of the
right eye, an “overall” correction.
Part II The surfacing chart gives 8.75 D for D1 and a4.1-mm center thickness for the right lens and11.00 D for D1 and a 5.7-mm center thickness for the left lens. Calculating the Ms from shape gives us the amount of magnification we would receive from
the lenses if the lenses were ordered as “stock” lenses: Ms = 8.75 × 4.1/15 = 2.4% for the right eye Ms = 11.00 × 5.7/15 = 4.2% for the left eye These lenses would give us a net 1.8% magnification on the left eye, not
at all what was required, which was 1% magnification on the right eye. Using the larger D1 and center thickness figure, place these amounts in the lines to the right
of Part II. (Using the identical curves and center thicknesses on
each lens would give zero magnification difference from Ms factor, which, while it is better than the stock lenses, is still not
the 1% magnification required for the right eye.) Decrease the front curve on the left lens to9.5 D. Recalculate Ms:
Ms = 9.5 × 5.7/15 = 3.6%
Part III Correct the Mp. For this change of D1, enter on line 3 the 1.5-D difference: 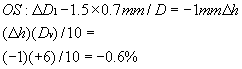
(This is a minification, since it represents a decrease in vertex distance.) The
magnification from Ms with this change in D1 is then 3.6% - 0.6% = 3.0%. The right lens is 4.2% and the left lens is now 3%, and the difference
is 1.2%, which is very close to the 1% needed. There is no need to change
t, center thickness. This is a practical endpoint. Discussion To decide which curve to use on the left lens for the front surface, I
first consulted the surfacing chart to see what curves are available that
are less than the 11.00-D curve on the right lens. I found these three
possible curves: 10.25, 9.50, and 8.75 D. The 10.25 D gives shape magnification of 10.25 × 5.7/15 = 3.9%, which
did not seem to be enoughof a change, whereas the 8.75-D curve was 8.75 × 5.7/15 = 3.3%. At first this seemed to be the curve of
choice, but when the power factor was calculated, the difference, (11.00 - 8.75) = 2.25 D, gave
a1.6-mm vertex distance change (2.25 × 0.7), and
this vertex distance change gives minification of 1.0%: (1.6)(+ 6.00)/10 = -1%. This 1% loss of magnification when added to the 3.3% would have resulted
in 2.3% for the left lens, and this when subtracted from 4.2% of the
right lens would become 1.9% magnification on the right eye, which is 0.9% too
much magnification. Recalculating, using the 9.5-D figure gave the correct answer. Other possibilities
include the following: - The curve on the right lens could have been increased to give the 1% magnification
needed for the right eye, but 11.00 D is already a very strongly
curved lens and any more added to it would make it appear strange. Had
the problem required more magnification than the 1%, this would
have been a feasible alternative, however.
- Increasing the center thickness on the right eye would also have been a
good suggestion, but increasing the center thickness would decrease the
vertex distance, which in turn would have caused a loss of magnification
from the power factor. It would also increase the weight of the
lens.
- With regard to the left lens, we could have decreased the center thickness
to attain less magnification, but again this would have been offset
by an increase in vertex distance, which would resultin more magnification. Also, in
the case of a thinner lens, care must be taken that the
edge thickness is not too thin or there will be danger of the lens
chipping, or the laboratory may even reject the instructions as being
impractical. For this reason it is wise to try to keep the lens size as
small as possible by encouraging the patient to select a frame with
a relatively small eye size.
EXAMPLE 2: MINUS LENS PROBLEM The right eye requires a -1.00-D lens and the left eye a -3.00-D lens. Vertex
distance, h, is 15 mm, and the lens will be 48 mm wide (Fig. 3). 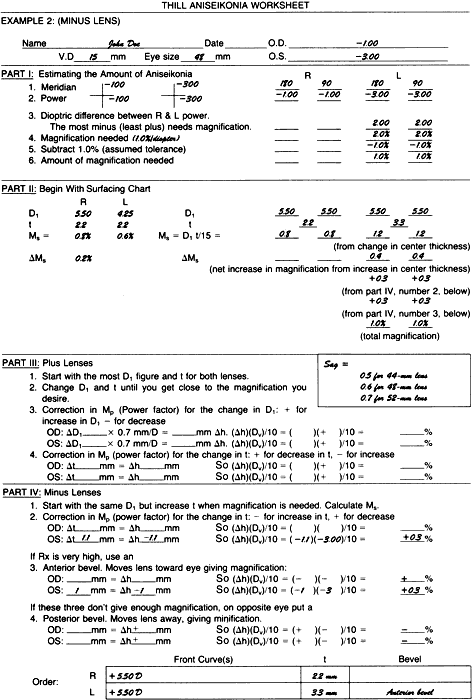 Fig. 3. Example 2: a minus lens problem. Fig. 3. Example 2: a minus lens problem.
|
Part I Using the same directions given in the plus lens problem of Figure 2, fill out Part I of the Thill Aniseikonia Worksheet down to line 6, the
amount of magnification needed, which in this example is 1% on the left
eye. Part II The surfacing chart indicates that at a 5.50-D curve would be used on the
right lens and a 4.25-D curve on the left lens, with both center thicknesses
being 2.2 mm. Calculating the Ms from shape gives us the amount of magnification we would receive from
the lenses if the stock lenses were ordered. Ms = 5.5 × 2.2/15 = 0.8% for the right eye Ms = 4.25 × 2.2/15 = 0.6% for the left eye Part IV Dropping down to the instructions for minus lenses, line 1 states to begin
with the same D1 for the front curves of both lenses and increase center thickness where
magnification is needed. Begin by first making both lenses the same:
| | R | L |
| D1 | 5.50 | 5.50 |
| t | 2.2 | 2.2 |
| Ms | 0.8% | 0.8% | and increase the center thickness on the left lens where the magnification
is required. If we increase to 3.3-mm center thickness, Ms becomes 5.5 × 3.3/15 = 1.2%. Comparing this with the right lens, we
now have 0.4% magnification on the left eye. We need 0.6% more. However, first
note the change in Mp (power factor). Line 2 is the correction in Mp for the change in t: 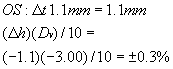
The increase in center thickness resulted in a decrease in vertex distance, which
in turn resulted in an increase in magnification (decrease
in minification) of 0.3%. This 0.3% when added to the 1.2% gives a total
magnification on the left eye of 1.5%. Subtracting the 0.8% magnification
of the right lens leaves a difference of 0.7%. This is an improvement, but
we still need 0.3% more magnification on the left eye. Part IV With an anterior bevel, we can move the lens toward the eye, giving magnification (decreased
minification). Request that the left lens be beveled
to the extreme anterior edge, which for a -3.00-D power lens and
a 48-mm diameter will have an edge thickness between 4 and 5 mm. If we
consider that this will amount to 1 mm: 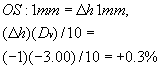
This 0.3% when added to the 1.5% equals 1.8%. Thus, the left lens now has
a magnification of 1.8%, which, when compared with the 0.8% magnification
of the right lens gives us the required net magnification of 1% in
the left lens. The order to the laboratory would be as follows: Rt lens: 5.50 D front curve; 2.2 mm t Lt lens: 5.50 D front curve; 3.3 mm
t, anterior bevel Discussion The right lens could have been decreased in its magnification. However, this
would be difficult since the power is low and the center thickness
is at the legal minimum limit. For example, if we tried to decrease the magnification of the right lens
by decreasing the front curve to 3.25 D:
Ms = 3.25 × 2.2/15 = 0.5%
or a decrease of 0.3%. This would be offset by the power factor change
of 5.50 - 3.25 = 2.25 D. And, 2.25 × 0.6 (for a 48-mm lens) = 1 mmthe lens moves closer to
the eye, and 1 mm(-1.00 D)/10 = 0.1% decrease in minification (increase
in magnification). So 0.5% plus 0.1% = 0.6% total magnification from
shape. Comparing this with the previous 0.8% shape magnification, we see that
decreasing the front curve to decrease the magnification resulted only
in a difference of 0.2% (0.8% - 0.6%). If we tried to increase the magnification of the left eye by increasing
the front curve (instead of increasing the center thickness as the example
showed), presume a 7.25-D front curve:
Ms = 7.25 × 2.2/15 = 1.06%
which does give about a 0.2% increase in magnification from shape, but
we lose 0.3% when we correct for power factor change: 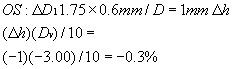
Since this represents a movement away from the eye, the result is a minification. Hence, the 1.06% figure must be decreased by this 0.3%, which
results in about 0.7%. This is slightly less magnification than the 0.8% we
had with the original 5.50-D and2.2-mm center thickness lens. Rule: On minus lenses, if the lens power is over -2.00 D, it is not possible
to get a net increase in magnification by changing the front curve. Some
magnification is achieved from the shape factor, but the power factor
has a greater influence, so the total effect of the two is a minification. Minus lenses thus present a special problem when trying to gain magnification. The
best solution is to work with the center thickness, increasing
this where magnification is needed, since this will give magnification
from both the shape factor, Ms, and the power factor, Mp. Next, if still more magnification on a minus lens is needed, decrease the
front curve on the eye needing the magnification. This further decreases
the vertex distance and adds to the magnification (decreases minification). There
will also be a slight change from the shape factor with
the flatter lens, but the power factor has more influence. Third, the bevel can be put on to the extreme front of the lens so that
the vertex distance is reduced as much as possible. Minus lenses, having
large edges, can be manipulated quite easily in this manner. If these three changes do not give the magnification needed, the lens of
the opposite eye (assuming it is also a minus lens) can be beveled to
the back to increase the vertex distance, thereby minifying that image. EXAMPLE 3: A CASE OF ASTIGMATISM The right eye requires + 1.00 – 3.00 × 180 and the left
eye requires plano -1.00 × 180. Vertex distance is 10 mm. Part I Put the powers on the optical cross, being certain they are in the correct
meridian. From the optical cross, transfer the powers to the correct
meridian in the columns. In this case, there is more minus in the right
eye in the vertical meridian and more minus (less plus) in the left
eye in the horizontal meridian. Magnification needed is 1% per diopter. There will be no allowance made
for tolerance, since this is astigmatic and tolerance is less than in
purely spherical cases. Part I should appear as shown in Figure 4.  Fig. 4. Example 3: a case of astigmatism. Fig. 4. Example 3: a case of astigmatism.
|
Begin with the surfacing chart. The lenses for these powers would be made
up with a curve on the right eye of 6.25 D and for the left eye of5.50 D. Center
thickness would be 2.3 mm for the right lens and 2.2 for
the left lens. Using this information as a starting point, flatten the
curves for the meridians where the least magnification is needed and
increase the curves for the meridians where the most magnification is
needed. There will therefore be two curves on the front of each lens. Keep
the center thicknesses the same and manipulate only the front curves. Part II will look something like shown in Figure 4. These lenses would be called bitoric because they have toric curves on both the front and the back surfaces. TRIAL ANISEIKONIC LENSES IN CLIP-ONS One way to determine if there is an aniseikonic condition without going
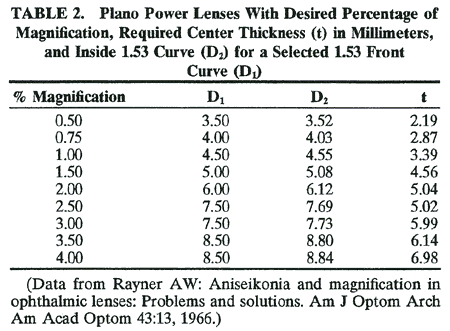
to the expense of first ordering aniseikonic lenses would be to use special
clip-on lenses that have magnification but no power. The configuration
for these lenses might be as shown in Table 2, although there could be other combinations to attain the same results.17
 |