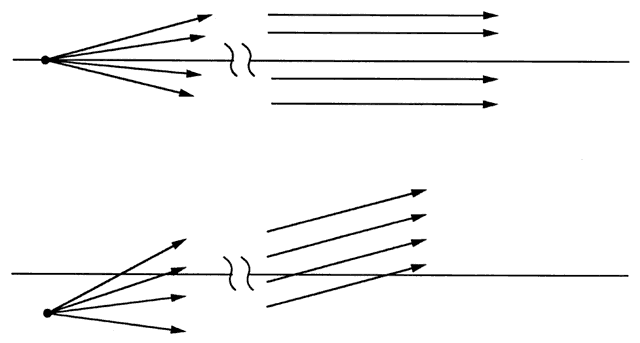
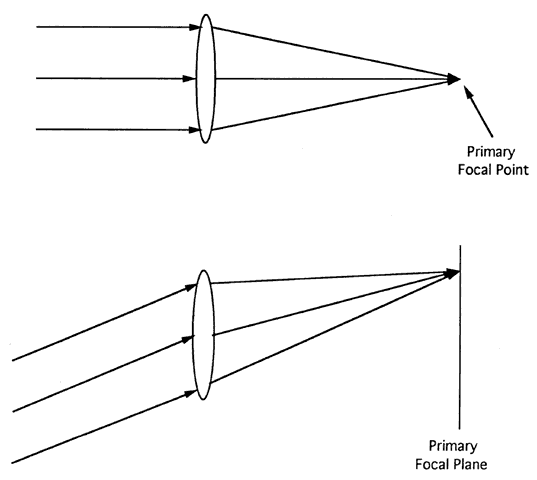
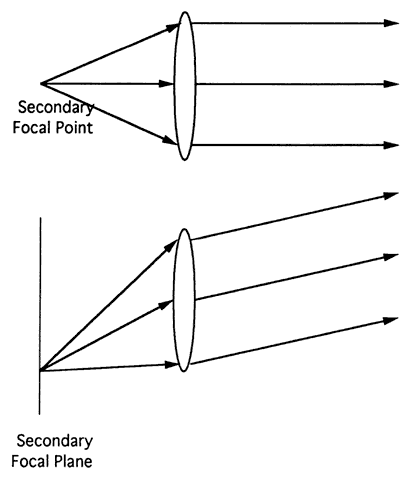
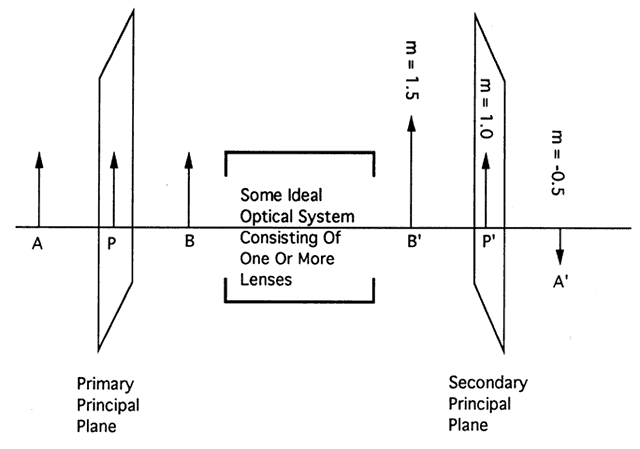
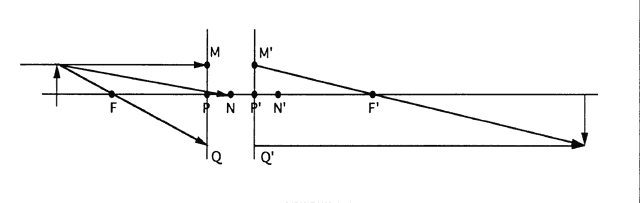
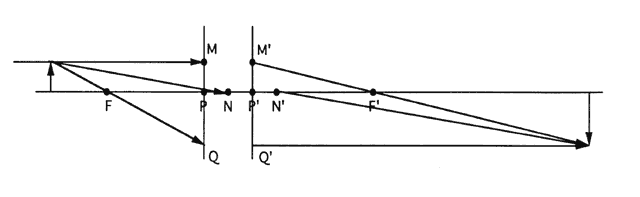
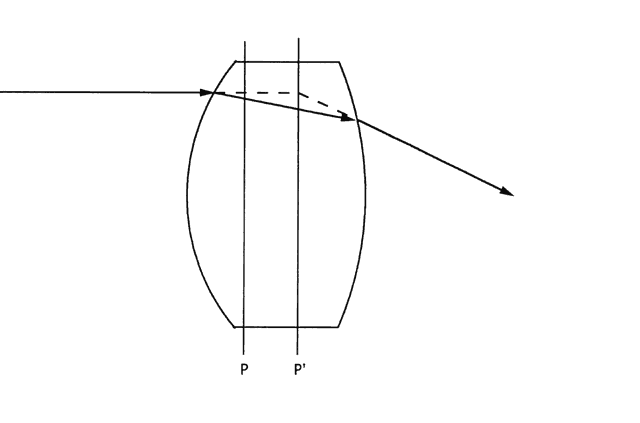
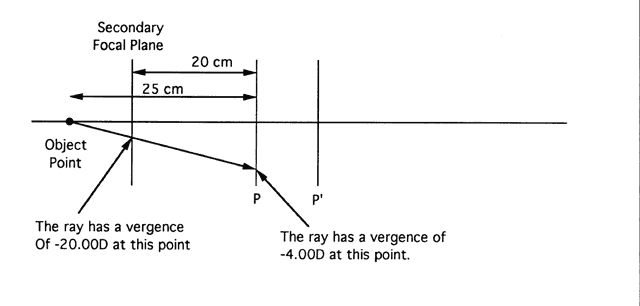
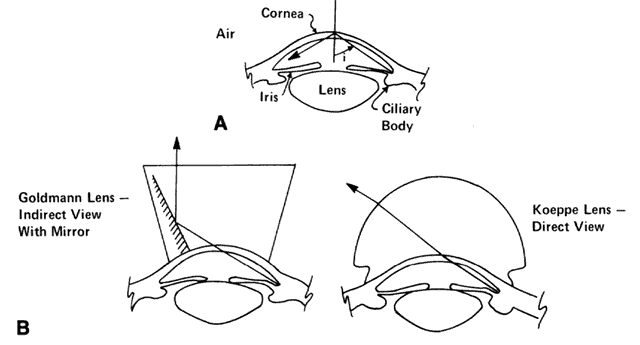
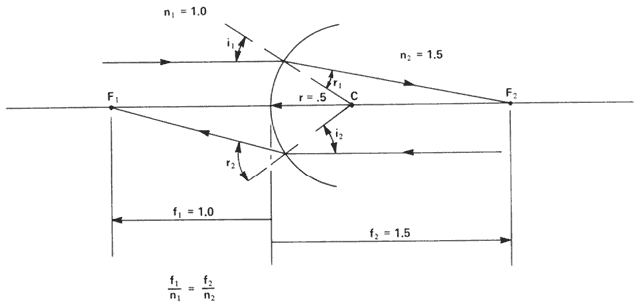
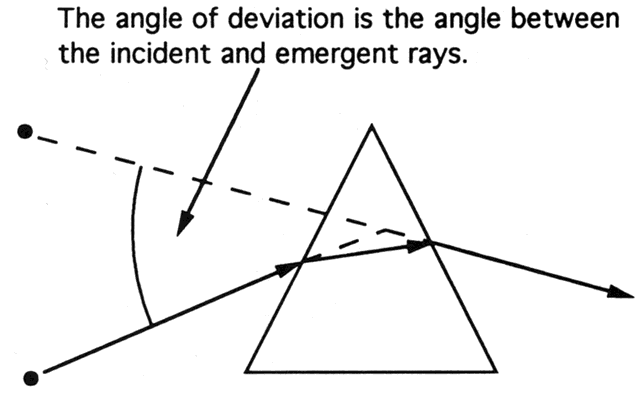
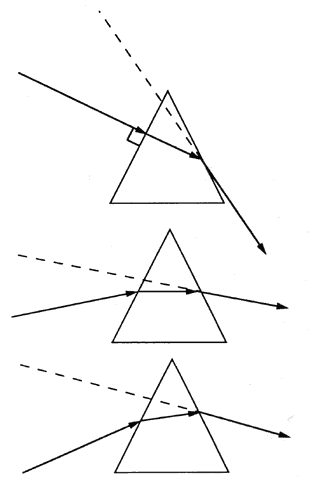
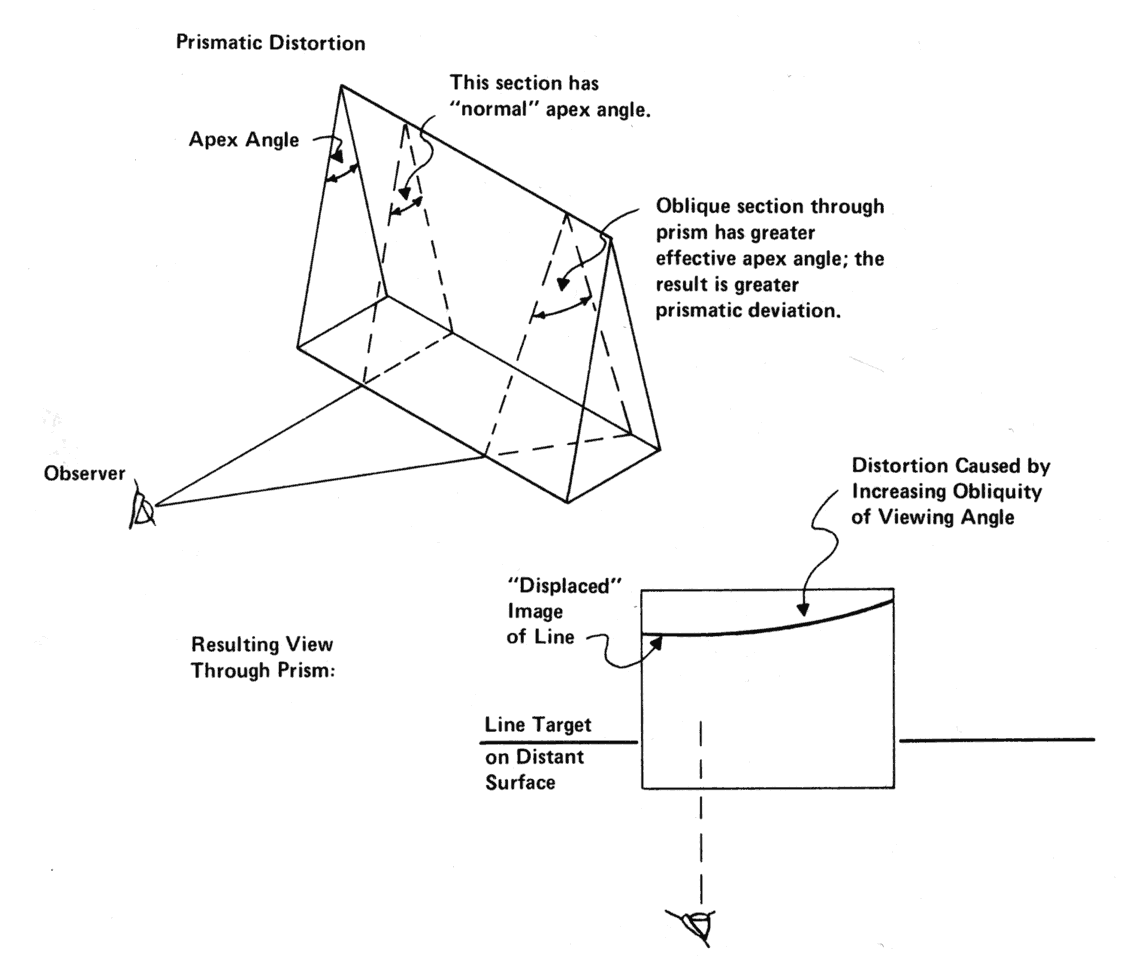
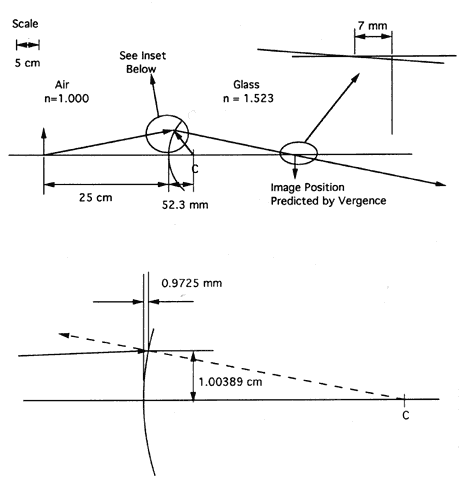
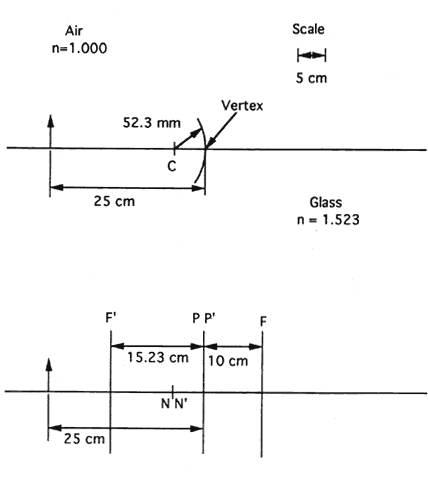
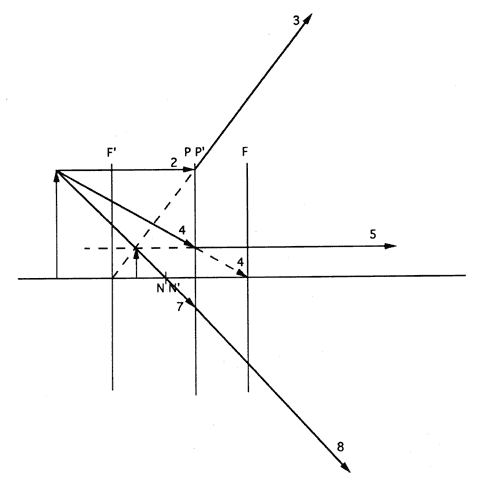
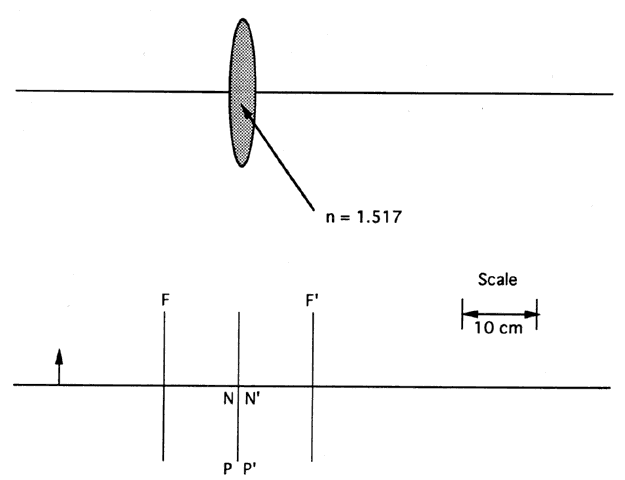
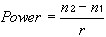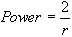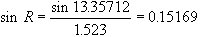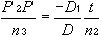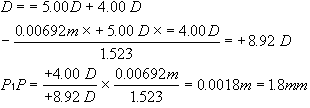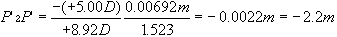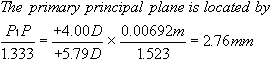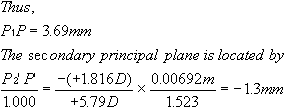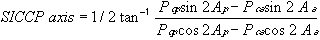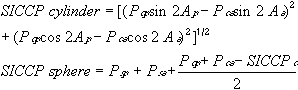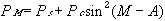| This section discusses some clinical applications of the preceding theory. It
is impossible to categorize all the clinical applications of optics. Pathology of the ocular media can be categorized on the basis of its effect
on image formation. There are three general classes of pathology: opaque
lesions, scattering or contrast-reducing lesions, and aberration-producing
lesions. Examples of opaque lesions include granular stromal dystrophy of the cornea, asteroid
hyalosis, and some types of congenital cataract. The important
clinical point is that opaque lesions do not affect vision unless
the pupil is almost completely obscured or unless the lesion is very
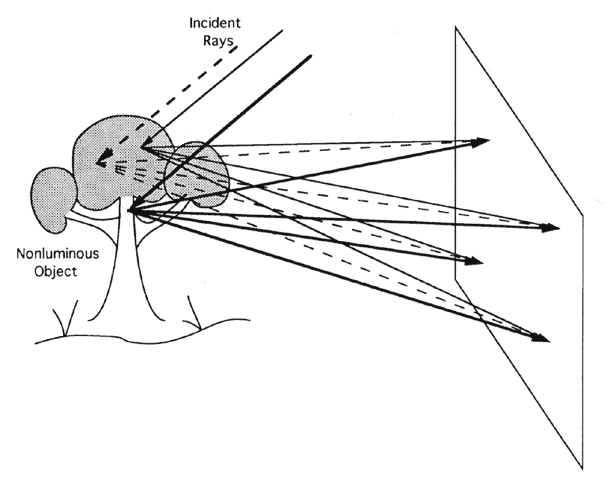
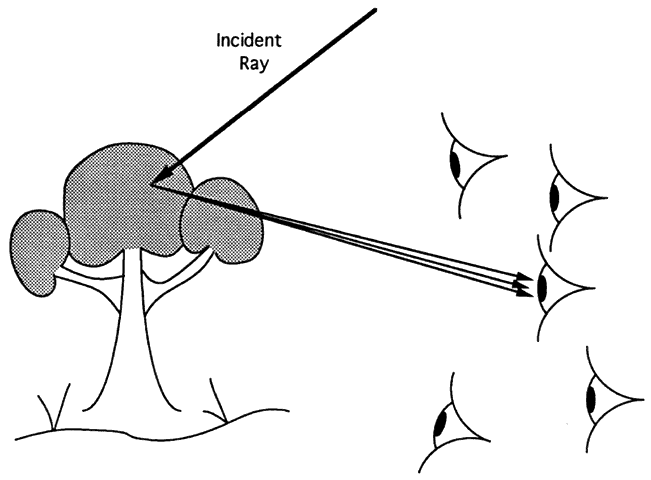
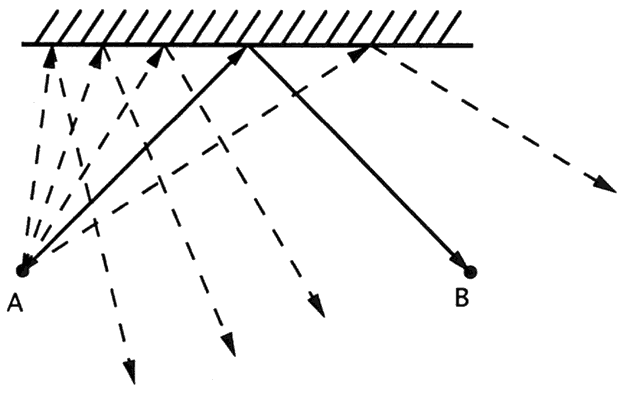
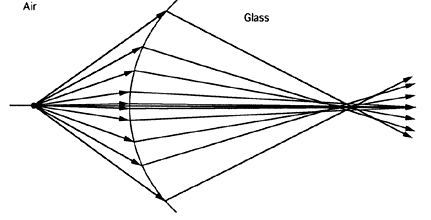
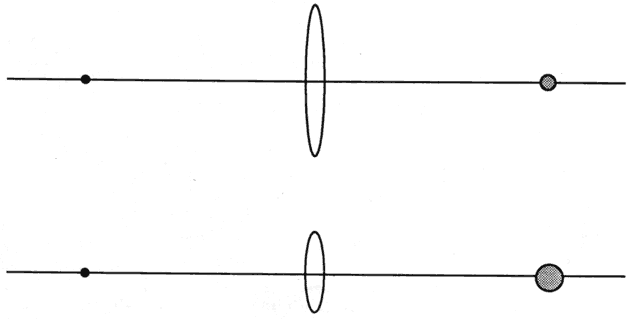
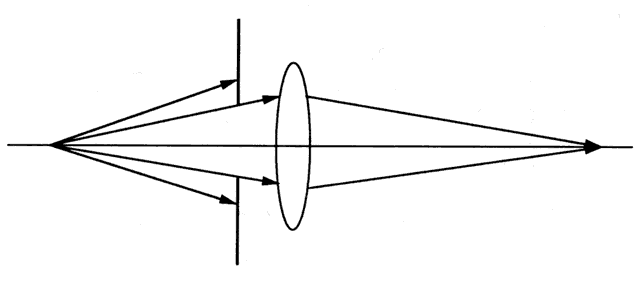
close to the retina. Place a piece of opaque tape in the center of a trial lens and image a
candle. The central obscuration has little effect on the image. Light
from each object point completely fills the lens (Fig. 81). A small opaque lesion blocks some of the light, but most still passes
through the lens. The light that does traverse the lens is still redirected
to produce a one-to-one correspondence between object and image. At
most, an opaque lesion produces a small decrease in image brightness, which, as
discussed previously, is barely noticeable. 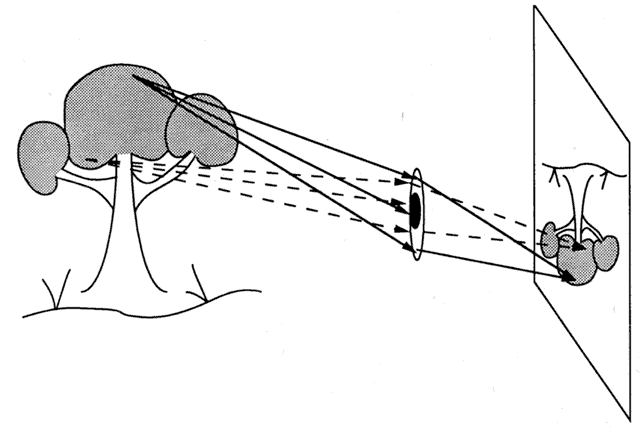 Fig. 81. An opaque lesion blocks some light, but light traversing the unaffected
part of the lens still forms an image. The image is slightly dimmer, but
otherwise unaffected. Fig. 81. An opaque lesion blocks some light, but light traversing the unaffected
part of the lens still forms an image. The image is slightly dimmer, but
otherwise unaffected.
|
Opaque lesions are usually quite apparent on slit lamp exam but may coexist
with other subtler pathology. Problems can arise if visual symptoms
are inappropriately attributed to opaque lesions. For example, a patient
with a crescent-shaped iris remnant on the lens (from an old posterior
synechia that was broken) presents with an arcuate scotoma. The
scotoma seemed to correspond to the shape of the iris remnant, which
was assumed to be the cause of the scotoma. Two years later, the patient
presented with advanced field loss and elevated intraocular pressure (IOP), and
the diagnosis of primary open-angle glaucoma was finally
made. When the patient initially presented, it would have been easy to constrict
the pupil so that the iris covered the remnant on the lens, and to
retest the visual field. If the scotoma had still been present, then
it clearly was not caused by the iris remnant. Unfortunately, simple maneuvers
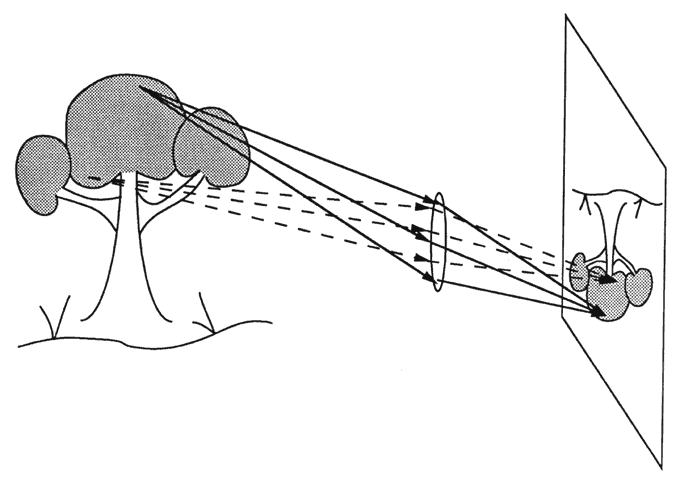
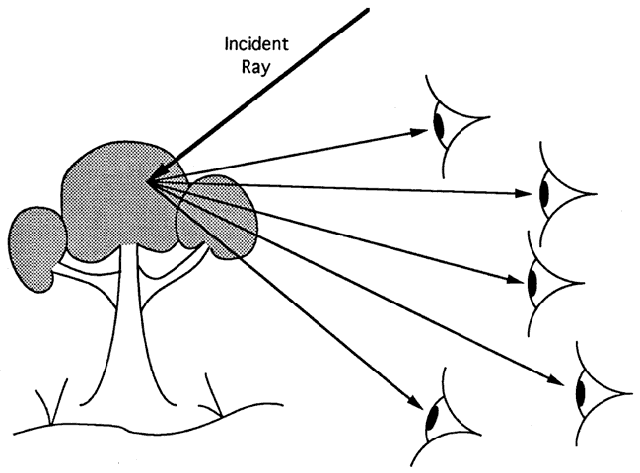
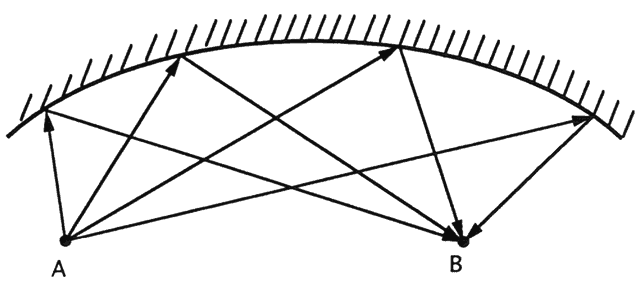
for diagnosing optical problems are often overlooked. Typical scattering lesions include vitreous hemorrhage, posterior capsular
cataract, and corneal edema. Light striking the abnormal area of the
media is not blocked as in opaque lesions. Light traverses the lesion
but is scattered in the process. The scattered light distributes generally
over the entire retina (Fig. 82). Light that passes through the normal parts of the ocular media still
creates an image on the retina, but the image is washed out by the scattered
light. The effect is similar to raising the house lights during
a movie, only more pronounced. Generally, vision is markedly affected, and
these are the easiest lesions to diagnose. Patients complain of
rainbows, halos, and glare. 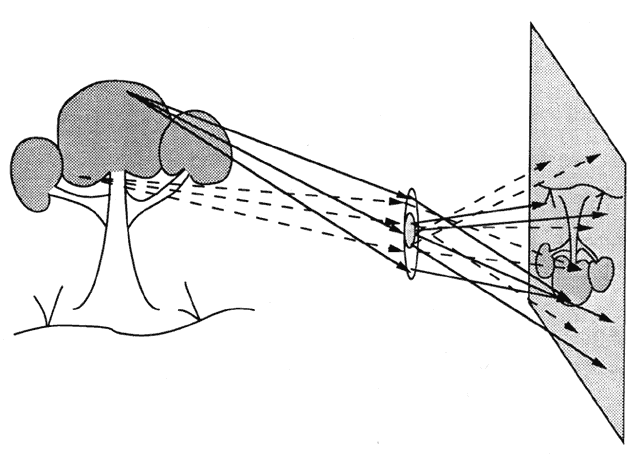 Fig. 82. Scattering lesions partially disrupt the one-to-one correspondence between
object and image by distributing some light randomly over the image. Light
that traverses the unaffected part of the lens still produces
an image, but the contrast is somewhat washed out. Fig. 82. Scattering lesions partially disrupt the one-to-one correspondence between
object and image by distributing some light randomly over the image. Light
that traverses the unaffected part of the lens still produces
an image, but the contrast is somewhat washed out.
|
Typical aberration-producing lesions include keratoconus, aphakia, subluxed
lenses, and postkeratoplasty astigmatism. As discussed, light from
a point source is distributed over a small region of the image instead
of being confined to a perfect point. Provided the light is spread
over only a small area, visual acuity is high. Aberration-increasing lesions
cause light from a point source to spread over an abnormally large
area and may cause the light distribution to become asymmetric. Patients with these problems often have near normal acuity but complain
of distinct visual phenomena. For example, spectacle-corrected aphakes
characteristically complain of pincushion distortion (doorways curve
in the middle, appearing too thin to pass through). The visual complaint
may be quite variable, depending on the cause of the aberration. Keratoconus
patients may complain of a variety of different phenomena because
each cone is a different shape and produces different aberrations. The
essential feature is not any aspect of the vision per se but rather
that the patient is able to describe in vivid detail the visual
experience. The visual complaint is specific, not vague. The patient can
often draw on paper the appearance of a point source, and this often
gives a clue to the problem. For example, patients post radial keratotomy (RK) may complain of “seeing” the
incisions. It was not until RKs were performed with
small numbers of incisions that it became clear that the “incisions” the
patient was “seeing” and the corneal incisions
were not in the same meridians. For instance, if the patient had
a four-incision RK with cuts in the 180 and 090 meridians, the patient
reported the “incisions he or she saw” in the 045 and 135 meridians. Moreover, some patients “saw” the incisions even
when the pupil was much smaller than the optical zone. The patient cannot be seeing the incisions. If the incisions are opaque, they
do not affect the image. If the incisions scatter light, then the
contrast is diminished, but this does not cause the patient to see
lines in specific meridians. In fact, the patient does not see the incisions
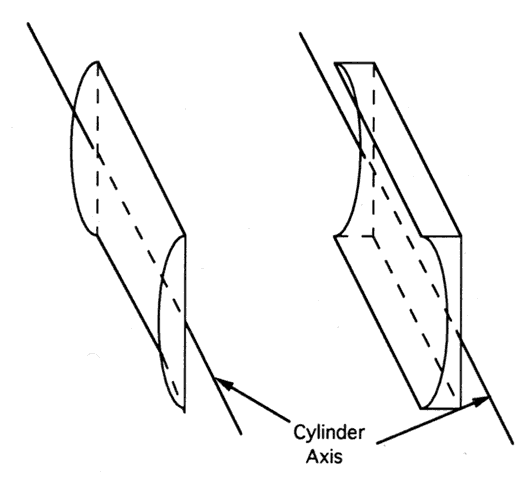
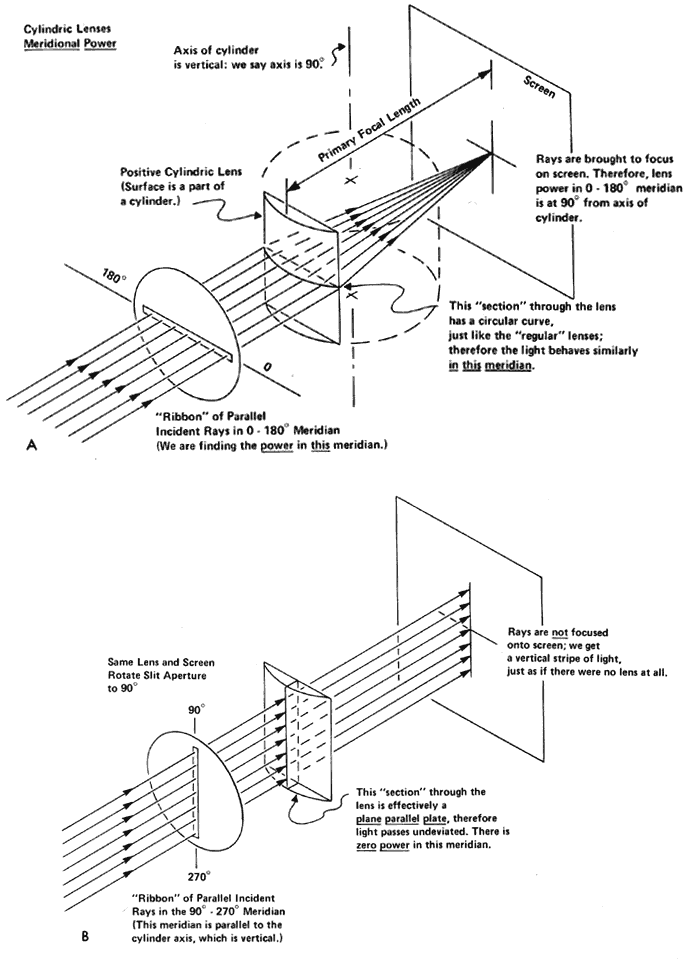
at all. The cornea retracts between the incisions, creating four
cylinders with axes in the meridians between the incisions (Fig. 83). These cylinders create the aberrant image that gives the mistaken impression
that the patient is “seeing the incisions.”  Fig. 83. A representation of the corneal surface after a four-incision radial keratotomy. The
incisions are in the valleys. The corneal tissue retracts
between incisions, causing the peaks that produce a “fourfold” form
of astigmatism. Fig. 83. A representation of the corneal surface after a four-incision radial keratotomy. The
incisions are in the valleys. The corneal tissue retracts
between incisions, causing the peaks that produce a “fourfold” form
of astigmatism.
|
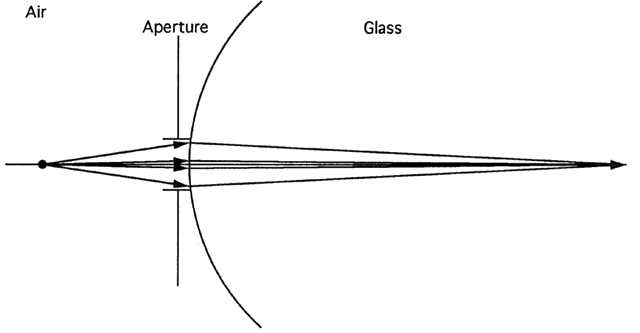
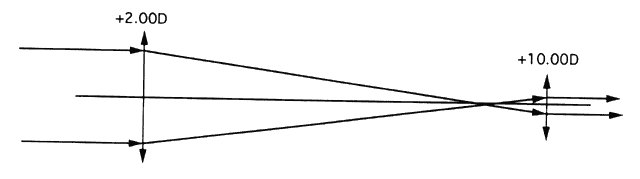
The importance of apertures is often overlooked. First, it is impossible
to selectively “look through” only part of the pupil. Consider
a patient with good acuity despite a dislocated intraocular lens (IOL) with
a positioning hole in the center of the pupil. The question
is often asked, “Which part of the pupil is the patient looking
through?” The answer is “all parts.” Light from an
object point fills the pupil, and some passes through the IOL, some
through the positioning hole, and some through the empty pupil. The patient
will see well if there is enough light focused on the retina to
yield an adequate image despite decreased contrast and possibly glare
from the optic's edges. If the patient does see well, it is not because
he or she is looking through only the IOL. Vision is preserved until late in the course of granular dystrophy because
the lesions are opaque and do not affect the retinal image until the
pupil is nearly totally obscured. However, some explain the preservation
of vision by assuming that the patient is somehow “pinholing” by
selectively looking through a small part of the cornea between
opaque lesions. If the patient were pinholing, then he or she would
have an unusually large depth-of-focus, and this could be demonstrated. Patients
with granular dystrophy do not exhibit increased depth-of-focus
until late in the disease when the pupil becomes nearly a single
pinhole. Of course, it is possible to move the eye so that one looks through only
a segment of a bifocal or trifocal spectacle. The eye moving independently
of a spectacle, or even a contact lens, can arrange its relatively
small pupil so that all the light passing through the pupil passes
through only one spectacle segment. The distinction between a bifocal
spectacle and a bifocal (or multifocal) IOL is important. At any one
time, a patient looks through either the distance or near segment of a
spectacle, so all the light on the retina is focused for either near
or far. However, with a bifocal IOL, light is always split between two
different images simultaneously. There is always some in-focus and some
out-of-focus light on the retina. The importance of the pupil in regulating retinal light levels is often
overstated. From dawn to high noon, the amount of ambient illumination
varies by thirteen orders of magnitude. The area of the pupil changes
by, at most, two orders of magnitude. The pupil may help compensate
for small transient fluctuations in illumination, but other mechanisms, such
as retinal adaptation, are much more important than the pupil for
adjusting to the large variation in light levels that we are exposed
to in the course of a day. Many factors besides light level influence pupil size, indicating that
the pupil has other roles than simply regulating retinal illumination. For
instance, the pupil constricts during accommodation. Clearly, this
is not to regulate retinal illumination, but it does increase depth-of-focus
and decrease spherical aberration. The pupil is also an important consideration in the prescription of visual
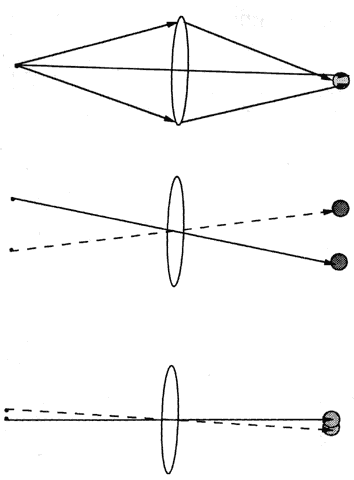
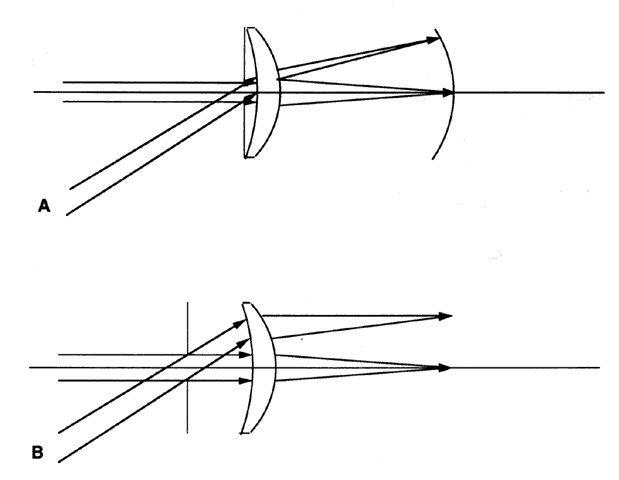
aids. Two important considerations are magnification and illumination. Galilean
telescopes produce upright images and are shorter than Keplerian
telescopes, making them attractive as a spectacle-mounted visual
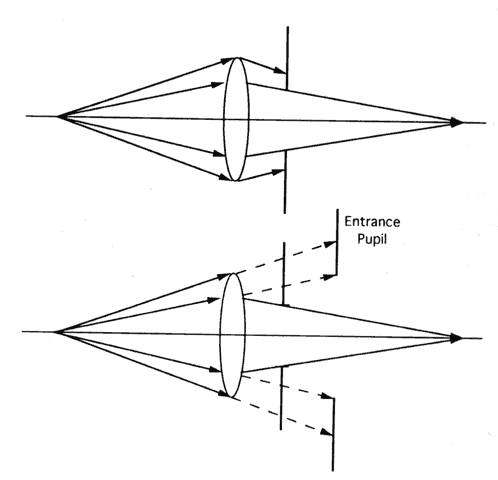
aid. However, the exit pupil is inside the telescope (Fig. 84). Because of this, some of the light emerging from the exit pupil of the
telescope misses the eye's entrance pupil. Thus, some of the light
entering the telescope is wasted, and the retinal illumination suffers. 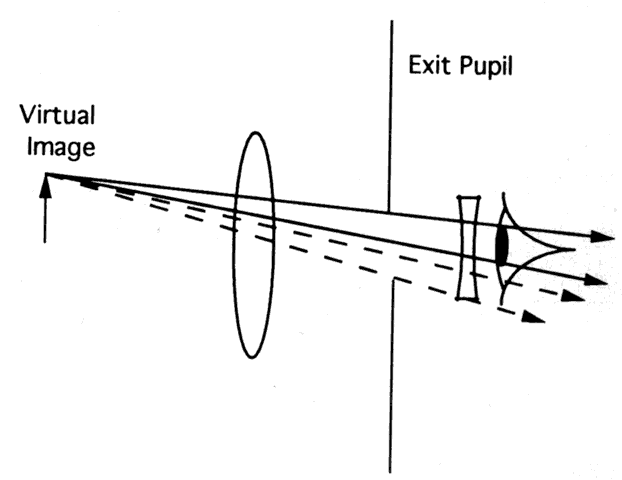 Fig. 84. In a typical Galilean telescope, the aperture stop and entrance pupil are
the edges of the objective lens. Thus, the exit pupil is inside the
telescope. Some of the light leaving the telescope necessarily fails
to enter the observer's eye (dotted lines) and is wasted. Fig. 84. In a typical Galilean telescope, the aperture stop and entrance pupil are
the edges of the objective lens. Thus, the exit pupil is inside the
telescope. Some of the light leaving the telescope necessarily fails
to enter the observer's eye (dotted lines) and is wasted.
|
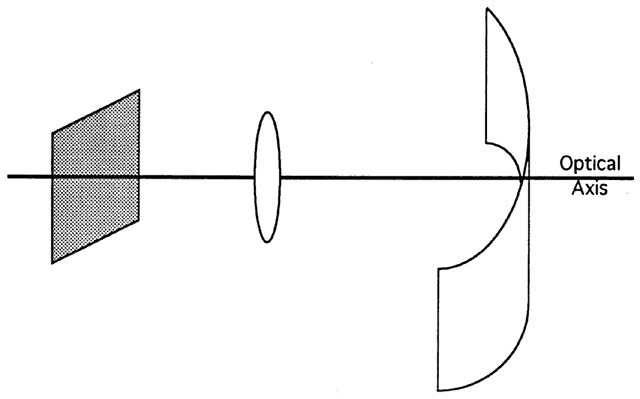
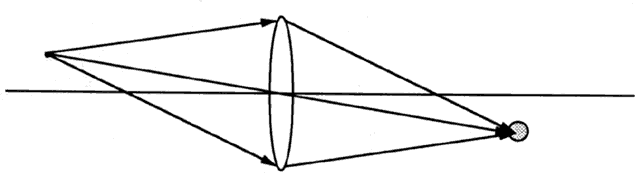
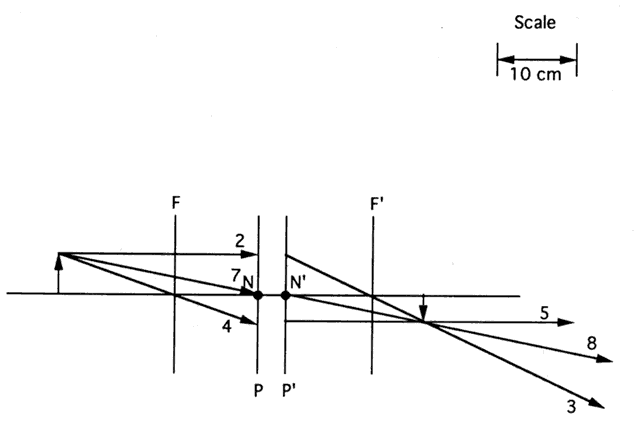
The Keplerian telescope is longer than the Galilean and heavier because
it must contain a prism assembly to erect the image that would otherwise
be inverted. These aspects make it unsuitable for a spectacle-mounted
visual aid. However, the exit pupil is behind the second lens (Fig. 85), so the user may place the exit pupil of the telescope in the entrance
pupil of his or her eye. Essentially all the light from the telescope
enters the eye. When a patient requires both a bright and enlarged image, a
hand-held Keplerian telescope may be the best choice. 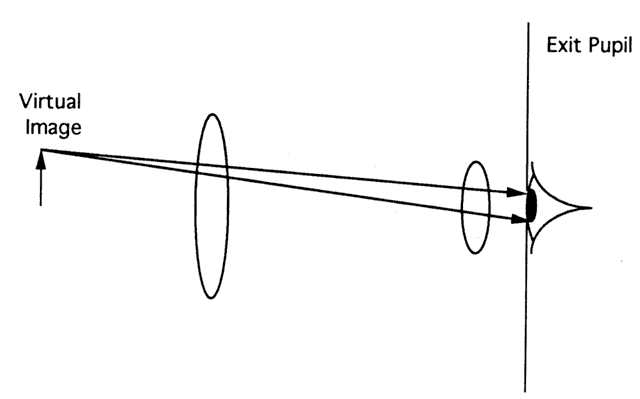 Fig. 85. In a typical astronomical telescope, the aperture stop and entrance pupil
are the edges of the objective lens. Thus, the exit pupil is behind
the telescope. Most of the light leaving the telescope enters the observer's
eye. Fig. 85. In a typical astronomical telescope, the aperture stop and entrance pupil
are the edges of the objective lens. Thus, the exit pupil is behind
the telescope. Most of the light leaving the telescope enters the observer's
eye.
|
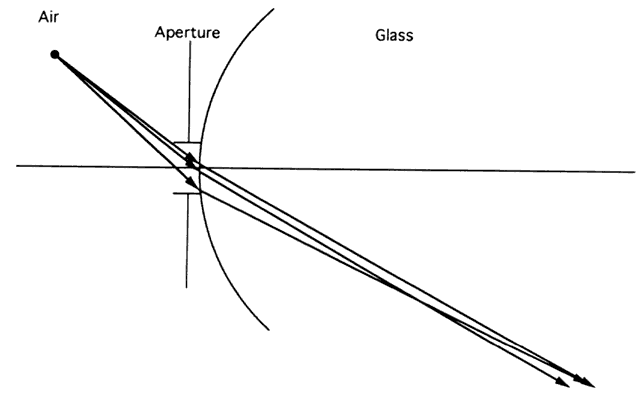
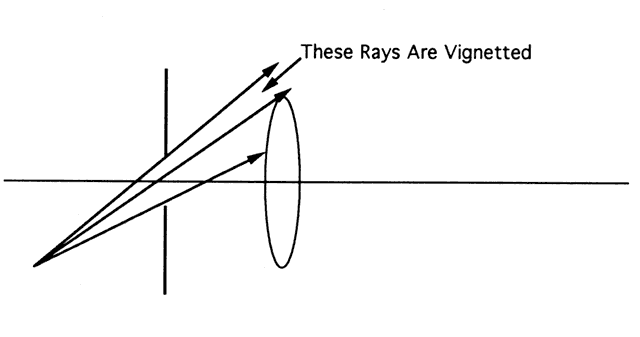
It is well known that miosis decreases the visual field. In theory, the
small pupil should decrease the general retinal illumination but not
alter the field. The decrease in field size is caused by the so-called
cosine drop-off law. The beam of light from off-axis points that reaches
the retina has a smaller cross-sectional area than the beam from on-axis
points (Fig. 86). Thus, less light from off-axis points reaches the retina. The visual
field is defined by the point where the amount of light reaching the
retina falls below threshold. The smaller the pupil, the smaller the field. 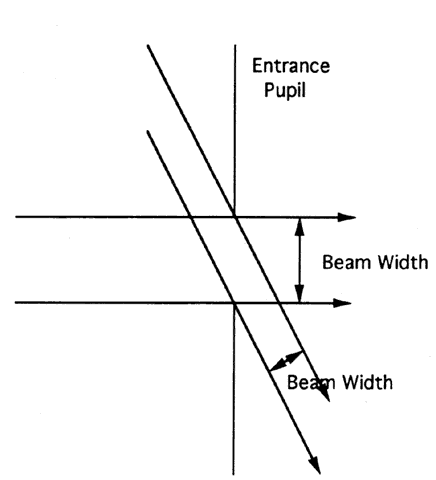 Fig. 86. The beam of light entering a system from off-axis points is much narrower
than that from on-axis points. Fig. 86. The beam of light entering a system from off-axis points is much narrower
than that from on-axis points.
|
Pupils play an important role in ophthalmoscopy. Direct ophthalmoscopy
is like looking into a room through an old-fashioned keyhole. The view
is limited (Fig. 87). The field-of-view can be enhanced by placing a lens in the keyhole to
form an image. This is the principle of indirect ophthalmoscopy, and
the fundus camera. Indirect ophthalmoscopy may be done binocularly or
monocularly. Thus, the essential distinction between direct and indirect
ophthalmoscopy is not binocularity. In direct ophthalmoscopy, the
observer directly views the retina. In indirect ophthalmoscopy, the observer
views an image of the retina. 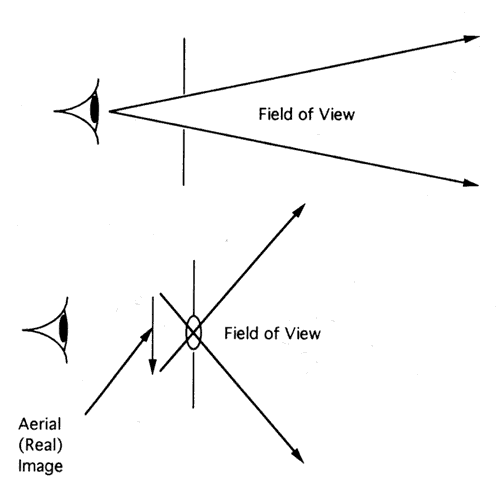 Fig. 87. The view through an external aperture may be quite limited. Placing a lens
in the aperture and viewing the resulting image increases the view. Fig. 87. The view through an external aperture may be quite limited. Placing a lens
in the aperture and viewing the resulting image increases the view.
|
In both types of ophthalmoscopy, the retina must be illuminated. The illumination
and viewing paths should be separate, or light reflected from
the cornea obscures the retinal image. Binocular ophthalmoscopy divides
the pupil of the eye under examination into three parts. Illumination
enters through one part, and each eye of the examiner views the retina
through another part (this arrangement is referred to as dark field illumination). The headpiece of the indirect ophthalmoscope contains two periscopes
that effectively shrink the examiner's interpupillary distance so
that both examiner's eyes can peer through separate parts of the
patient's pupil. The size of the retinal image in indirect ophthalmoscopy depends on the
power of the condensing lens. The lower the lens power, the larger the
image. Examination of the disc is enhanced by the increased axial magnification
that accompanies a larger transverse magnification. Because
axial magnification increases as roughly the square of the transverse
magnification, some examiners use a + 14.00 D instead of the standard + 20.00 D
lens to examine the disc for cupping. Other chapters describe the optics of devices commonly used in clinical
practice. The effective use of these instruments requires a knowledge
of their operating principles. |